题目内容
三棱锥P-ABC中，PA⊥平面ABC，PA=AB，则直线PB与平面ABC所成的角等于考点：直线与平面所成的角
专题：空间角
分析：利用线面垂直的性质得到：∠PAB就是直线PB与平面ABC所成的角．再根据PA=AB，进一步求出结果．
解答：
解：三棱锥P-ABC中，PA⊥平面ABC，
∠PAB=90°
所以：∠PAB就是直线PB与平面ABC所成的角．
又PA=AB
所以：∠PAB=45°
故答案为：45°
∠PAB=90°
所以：∠PAB就是直线PB与平面ABC所成的角．
又PA=AB
所以：∠PAB=45°
故答案为：45°
点评：本题考查的知识要点：线面的夹角，线面垂直的性质，属于基础题型．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
设非空集合P，Q满足P∩Q=P，则（ ）
| A、?x∈Q，有x∈P |
| B、?x∉Q，有x∉P |
| C、?x0∉Q，使得x0∈P |
| D、?x0∈P，使得x0∉P |
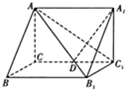如图所示，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AB=2，BC=1，D是棱CC1的中点，A1D⊥AB1；