题目内容
已知圆和y轴相切,且圆心在直线x-3y=0上,且被直线y=x截得弦长为
,求这个圆的方程.
| 7 |
考点:圆的标准方程
专题:计算题,直线与圆
分析:设出圆的方程,然后根据圆与y轴相切得到圆心到y轴的距离求出半径,利用直线y=x截得弦长为
,结合勾股定理,即可求出圆的方程.
| 7 |
解答:
解:设圆方程为(x-3b)2+(y-b)2=9b2,l为弦长,d为圆心到直线的距离,则r2=(
)2+d2,
∴9b2=(
)2+(
)2⇒b=±
,
∴所求圆的方程为(x-
)2+(y-
)2=
或(x+
)2+(y+
)2=
.
| 1 |
| 2 |
∴9b2=(
| ||
| 2 |
| |3b-b| | ||
|
| 1 |
| 2 |
∴所求圆的方程为(x-
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
点评:本题考查用待定系数法求圆的方程,一般可通过已知条件,设出所求方程,再寻求方程组进行求解.

练习册系列答案
相关题目
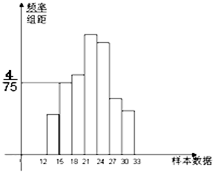 如图是总体的一个样本频率分布直方图,且在[15,18)内频数为8,在[12,15)内的小矩形面积为0.1.
如图是总体的一个样本频率分布直方图,且在[15,18)内频数为8,在[12,15)内的小矩形面积为0.1. 如图,长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接B1C,过B作B1C的垂线交CC1于E,交B1C于F,
如图,长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接B1C,过B作B1C的垂线交CC1于E,交B1C于F,