题目内容
对a、b>0,a≠b,已知下列不等式成立:
①2ab<a2+b2;②ab2+a2b<a3+b3;
③ab3+a3b<a4+b4;④ab4+a4b<a5+b5.
(1)用类比的方法写出 <a6+b6;
(2)若a、b>0,a≠b,证明:ab2+a2b<a3+b3;
(3)将上述不等式推广到一般情形,请写出你所得结论的数学表达式(不必证明).
①2ab<a2+b2;②ab2+a2b<a3+b3;
③ab3+a3b<a4+b4;④ab4+a4b<a5+b5.
(1)用类比的方法写出
(2)若a、b>0,a≠b,证明:ab2+a2b<a3+b3;
(3)将上述不等式推广到一般情形,请写出你所得结论的数学表达式(不必证明).
考点:类比推理
专题:计算题,推理和证明
分析:(1)类比答案不唯一,得出的结论不一定正确,(2)作差证明,(3)归纳推理得到的结论也不一定正确.
解答:
解:(1)类比得到:ab5+a5b<a6+b6;(或a2b4+a4b2<a6+b6或2a3b3<a6+b6);
(2)∵a3+b3-(a2b+ab2)=a3+b3-a2b-ab2=a2(a-b)+b2(b-a)
=(a-b)(a2-b2)=(a-b)2(a+b)
又∵a,b>0,a≠b,
∴a+b>0,(a-b)2>0,
∴a3+b3-(a2b+ab2)>0
∴a2b+ab2<a3+b3.
(3)一般情形为:ambn+anbm<am+n+bm+n(a>0,b>0,a≠b,m,n∈N*).
(2)∵a3+b3-(a2b+ab2)=a3+b3-a2b-ab2=a2(a-b)+b2(b-a)
=(a-b)(a2-b2)=(a-b)2(a+b)
又∵a,b>0,a≠b,
∴a+b>0,(a-b)2>0,
∴a3+b3-(a2b+ab2)>0
∴a2b+ab2<a3+b3.
(3)一般情形为:ambn+anbm<am+n+bm+n(a>0,b>0,a≠b,m,n∈N*).
点评:本题考查了类比推理及归纳推理,其结论的正确性要通过证明才可以.

练习册系列答案
相关题目
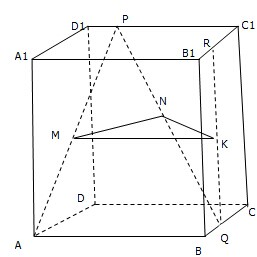 如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.
如图,在正方体ABCD-A1B1C1D1中,P、Q、R分别为棱D1C1、BC、B1C1上异于顶点的点,M、N、K分别为线段AP、PQ、QR的中点,求证:平面MNK∥平面ABCD.