题目内容
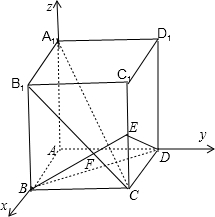
 如图,长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接B1C,过B作B1C的垂线交CC1于E,交B1C于F,
如图,长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,连接B1C,过B作B1C的垂线交CC1于E,交B1C于F,(1)求证:A1C⊥平面EBD;
(2)求点A到平面A1B1C的距离;
(3)求直线DE与平面 A1B1C所成角的正弦值.
考点:直线与平面垂直的判定,直线与平面所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)首先建立空间直角坐标系,求出空间点的坐标,向量的坐标,进一步证明线面垂直.
(2)先求出平面的法向量,进一步利用d=
求出距离.
(3)利用向量的夹角公式求解,但要注意用绝对值.
(2)先求出平面的法向量,进一步利用d=
|
| ||||
|
|
(3)利用向量的夹角公式求解,但要注意用绝对值.
解答:
证明:如图建立空间直角坐标系A-xyz.
(1)A(0,0,0,),A1(0,0,2),E(1,1,
),B(1,0,0),
D(0,1,0),C(1,1,0),
∴
=(1,1,-2)
=(0,1,
)
=(1,0,
)
∴
•
=0
•
=0
即A1C⊥BE A1C⊥DE
∵BE∩DE=E
∴A1C⊥平面EBD
(2)设平面A1B1C的一个法向量为
=(x,y,z),
则∴,令z=1,得
=(0,2,1).
∵
=(0,0,2),
所以,根据点到直线间的距离公式:d=
=
.
(3)由(2)知,得
=(0,2,1).
∵
=(-1,0,-
)
设
与
所成角为θ,则 sinθ=|cos<
,
>|=
=
(1)A(0,0,0,),A1(0,0,2),E(1,1,
| 1 |
| 2 |
D(0,1,0),C(1,1,0),
∴
| A1C |
| BE |
| 1 |
| 2 |
| DE |
| 1 |
| 2 |
∴
| A1C |
| BE |
| A1C |
| DE |
即A1C⊥BE A1C⊥DE
∵BE∩DE=E
∴A1C⊥平面EBD
(2)设平面A1B1C的一个法向量为
| m |
则∴,令z=1,得
| m |
∵
| AA1 |
所以,根据点到直线间的距离公式:d=
|
| ||||
|
|
| 2 |
| 5 |
| 5 |
(3)由(2)知,得
| m |
∵
| ED |
| 1 |
| 2 |
设
| ED |
| m |
| m |
| ED |
|
| ||||
|
|
| 1 |
| 5 |

点评:本题考查的知识点;空间直角坐标系,线面垂直的判定低定理,向量垂直的充要条件,直线与平面所成的角,点面的距离公式,向量的夹角公式,属于高考常见题型.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目