题目内容
已知x>0,y>0,
+
=1,则2x+y最小值为 .
| 1 |
| x |
| 1 |
| y |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:2x+y=(2x+y)(
+
),化简后利用基本不等式可求.
| 1 |
| x |
| 1 |
| y |
解答:
解:∵x>0,y>0,
+
=1,
∴2x+y=(2x+y)(
+
)=3+
+
≥3+2
=3+2
,
当且仅当
=
时取等号,
由
解得x=1+
,y=
+1,
∴2x+y最小值为3+2
,
故答案为:3+2
.
| 1 |
| x |
| 1 |
| y |
∴2x+y=(2x+y)(
| 1 |
| x |
| 1 |
| y |
| y |
| x |
| 2x |
| y |
|
| 2 |
当且仅当
| y |
| x |
| 2x |
| y |
由
|
| ||
| 2 |
| 2 |
∴2x+y最小值为3+2
| 2 |
故答案为:3+2
| 2 |
点评:该题考查利用基本不等式求函数的最值,属基础题.变形:2x+y=(2x+y)(
+
)是解决本题的关键所在.
| 1 |
| x |
| 1 |
| y |

练习册系列答案
相关题目
不等式|2x-1|>3的解集是( )
| A、{x|-1<x<2} |
| B、{x|-2<x<1} |
| C、{x|x>2或x<-1} |
| D、{x|x>-1或x<2} |
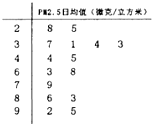 世卫组织规定,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.清远市环保局从市区2013年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),从这15天的数据中任取3天的数据,则恰有一天空气质量达到一级的概率为
世卫组织规定,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.清远市环保局从市区2013年全年每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶),从这15天的数据中任取3天的数据,则恰有一天空气质量达到一级的概率为