题目内容
已知f(x)=2+log3x,x∈[1,9]
(1)求y=[f(x)]2+f(x2)的定义域;
(2)求y=[f(x)]2+f(x2)的最大值及当y取最大值时x的值.
(1)求y=[f(x)]2+f(x2)的定义域;
(2)求y=[f(x)]2+f(x2)的最大值及当y取最大值时x的值.
考点:复合函数的单调性
专题:函数的性质及应用
分析:(1)把f(x)=2+log3x代入y=[f(x)]2+f(x2)得到函数的解析式,由
求得函数的定义域;
(2)令u=log3x换元,然后利用配方法求函数的最大值并求得当y取最大值时x的值.
|
(2)令u=log3x换元,然后利用配方法求函数的最大值并求得当y取最大值时x的值.
解答:
解:(1)∵f(x)=2+log3x,
∴y=[f(x)]2+f(x2)=(2+log3x)2+(2+log3x2)
=log32x+6log3x+6=(log3x+3)2-3.
∵函数f(x)的定义域为[1,9],
∴要使函数y=[f(x)]2+f(x2)有定义,
则
,∴1≤x≤3,
即函数定义域为[1,3];
(2)令u=log3x,则0≤u≤1.
y=(log3x+3)2-3=(u+3)2-3,
又∵函数y=(u+3)2-3在[-3,+∞)上是增函数,
∴当u=1时,函数y=(u+3)2-3有最大值13.
即当log3x=1,x=3时,函数y=[f(x)]2+f(x2)有最大值为13.
∴y=[f(x)]2+f(x2)=(2+log3x)2+(2+log3x2)
=log32x+6log3x+6=(log3x+3)2-3.
∵函数f(x)的定义域为[1,9],
∴要使函数y=[f(x)]2+f(x2)有定义,
则
|
即函数定义域为[1,3];
(2)令u=log3x,则0≤u≤1.
y=(log3x+3)2-3=(u+3)2-3,
又∵函数y=(u+3)2-3在[-3,+∞)上是增函数,
∴当u=1时,函数y=(u+3)2-3有最大值13.
即当log3x=1,x=3时,函数y=[f(x)]2+f(x2)有最大值为13.
点评:本题考查了复合函数定义域的求法,考查了复合函数的单调性,训练了利用换元法求函数的值域,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,c=4,a=2,C=45°,则sinA等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
等差数列{an}中,已知前15项的和S15=90,则a8等于( )
A、
| ||
| B、12 | ||
| C、6 | ||
D、
|
等差数列{an}的前n项和为Sn,若a2+a4+a6=12,则S7的值是( )
| A、28 | B、24 | C、21 | D、7 |
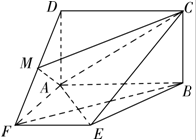 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.