题目内容
求过点M(-3,2),离心率为
的双曲线C的方程.
| 2 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:因为离心率为
的双曲线为等轴双曲线,所以设双曲线方程为x2-y2=λ(λ≠0),又双曲线过M(-3,2),即可求得λ的值,得到双曲线的标准方程.
| 2 |
解答:
解:设离心率为
的双曲线C的方程为x2-y2=λ(λ≠0)
将M(-3,2),代入双曲线方程得λ=5,
∴双曲线的标准方程为
-
=1.
| 2 |
将M(-3,2),代入双曲线方程得λ=5,
∴双曲线的标准方程为
| x2 |
| 5 |
| y2 |
| 5 |
点评:本题主要考查了等轴双曲线的方程的求法,做题时应用到等轴双曲线可设为x2-y2=λ(λ≠0).

练习册系列答案
相关题目
已知双曲线x2-
=1,过点P(2,4)的直线l与双曲线有且仅有一个公共点,则这样的直线l共有.( )
| y2 |
| 4 |
| A、0条 | B、2条 | C、3条 | D、4条 |
函数f(x)=-2sin2x-8sinx的最大值是( )
| A、0 | B、4 | C、6 | D、7 |
若函数y=ax+b的部分图象如图所示,则( )
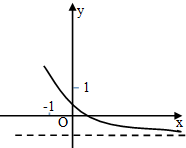

| A、0<a<1,-1<b<0 |
| B、0<a<1,0<b<1 |
| C、a>1,-1<b<0 |
| D、a>1,-1<b<0 |
二项式(1+x)n的展开式中,只有第七项的二项式系数最大,那么正整数n的值为( )
| A、10 | B、11 | C、12 | D、13 |