题目内容
5．用计算器求在0°～360°范围内的角x（精确到0.01°）：（1）cosx=0.12；（2）sinx=0.45．
分析 由条件利用反正弦函数、反余弦函数的定义，求得x的值．
解答 解：（1）∵cosx=0.12，x∈[0，2π），∴x=arccos0.12，或 x=2π-arccos0.12．
（2）∵sinx=0.45，x∈[0，2π），∴x=arcsin0.45，或 x=π-arcsin0.45．
点评 本题主要考查反正弦函数、反余弦函数的定义，属于基础题．
练习册系列答案
活力课时同步练习册系列答案
相关题目
16．函数f（x）=x|x|是（ ）
| A． | 偶函数且增函数 | B． | 偶函数且减函数 | C． | 奇函数且增函数 | D． | 奇函数且减函数 |
20．已知抛物线C：y2=2px（p＞0），直线l与抛物线C交于A，B两点（不同于原点），以AB为直径的圆过坐标原点O，则关于直线l的判断正确的是（ ）
| A． | 过定点（4p，0） | B． | 过定点（2p，0） | C． | 过定点（p，0） | D． | 过抛物线焦点 |
10．在正方体ABCD-A1B1C1D1中，E、F分别为AB、C1D1的中点，则A1B1与平面A1EF夹角的正弦值为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{\sqrt{6}}{4}$ | D． | $\sqrt{2}$ |
14．图中阴影部分的面积用定积分表示为（ ）
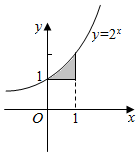
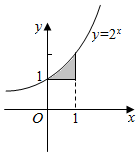
| A． | ${∫}_{0}^{1}$2xdx | B． | ${∫}_{0}^{1}$（2x-1）dx | C． | ${∫}_{0}^{1}$（2x+1）dx | D． | ${∫}_{0}^{1}$（1-2x）dx |