题目内容
下列命题中,正确的一个是( )
| A、?x0∈R,ln(x02+1)<0 | ||
| B、?x>2,x2>2x | ||
| C、若q是¬p成立的必要不充分条件,则¬q是p成立的充分不必要条件 | ||
D、若x≠kπ(k∈Z),则sin2x+
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.由于
+1≥1,可得ln(
+1)≥0,即可判断出不正确;
B.取x=4>2,x2=2x=16,即可否定;
C.由于q是¬p成立的必要不充分条件,其逆否命题为p是¬q成立的必要不充分条件,进而判断出;
D.取sinx=-
,则sin2x+
<0,即可否定.
| x | 2 0 |
| x | 2 0 |
B.取x=4>2,x2=2x=16,即可否定;
C.由于q是¬p成立的必要不充分条件,其逆否命题为p是¬q成立的必要不充分条件,进而判断出;
D.取sinx=-
| 1 |
| 100 |
| 2 |
| sinx |
解答:
解:A.∵
+1≥1,∴ln(
+1)≥0,因此不存在x0∈R,ln(x02+1)<0,不正确;
B.取x=4>2,x2=2x=16,因此不正确;
C.由于q是¬p成立的必要不充分条件,其逆否命题为p是¬q成立的必要不充分条件,因此¬q是p成立的充分不必要条件,正确;
D.∵x≠kπ(k∈Z),取sinx=-
,则sin2x+
<0,因此不正确.
故选:C.
| x | 2 0 |
| x | 2 0 |
B.取x=4>2,x2=2x=16,因此不正确;
C.由于q是¬p成立的必要不充分条件,其逆否命题为p是¬q成立的必要不充分条件,因此¬q是p成立的充分不必要条件,正确;
D.∵x≠kπ(k∈Z),取sinx=-
| 1 |
| 100 |
| 2 |
| sinx |
故选:C.
点评:本题考查了函数的性质、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
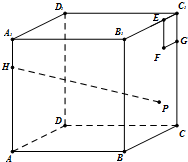 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )| A、21 | B、22 | C、23 | D、25 |
若a=
,b=lgπ,c=e-
,则( )
| 1 |
| sin7 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<a<b |
| C、b<a<c |
| D、b<c<a |