题目内容
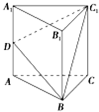 如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )
如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:依题意,设底边长为a,高为b,则C1D2=A1D2+A1C12=
+a2,BD2=AD2+AB2=
+a2,∠DC1B=45°,△BC1D的面积S=6,从而得到b2=16,a2=8,由此能求出此三棱柱的体积.
| b2 |
| 4 |
| b2 |
| 4 |
解答:
解:依题意,设底边长为a,高为b,
则在Rt△A1DC1中,C1D2=A1D2+A1C12=
+a2,
在Rt△ABD中,BD2=AD2+AB2=
+a2,
C1D2=BD2,C1D=BD,∠C1DB=90°,
∠DC1B=∠DBC1=
(180°-∠BDC1)=
(180°-90°)=45°,
△BC1D的面积S=
(BD×C1D)=
BD2=6,
BD2=12,BD=2
=C1D,
C1B2=C1D2+BD2=2BD2,C1B=
BD=2
,
在Rt△BCC1中,C1B2=BC2+CC12=a2+b2=(2
)2=24,
a2=24-b2,
BD2=
+a2=12,a2=12-
=24-b2,
=12,b2=16,b=4,a2=24-b2=24-16=8,
△ABC为等边三角形,它的面积为
a2sin60°=2
,
∴此三棱柱的体积V=S△ABC×AA1=2
×4=8
.
故选:B.

则在Rt△A1DC1中,C1D2=A1D2+A1C12=
| b2 |
| 4 |
在Rt△ABD中,BD2=AD2+AB2=
| b2 |
| 4 |
C1D2=BD2,C1D=BD,∠C1DB=90°,
∠DC1B=∠DBC1=
| 1 |
| 2 |
| 1 |
| 2 |
△BC1D的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
BD2=12,BD=2
| 3 |
C1B2=C1D2+BD2=2BD2,C1B=
| 2 |
| 6 |
在Rt△BCC1中,C1B2=BC2+CC12=a2+b2=(2
| 6 |
a2=24-b2,
BD2=
| b2 |
| 4 |
| b2 |
| 4 |
| 3b2 |
| 4 |
△ABC为等边三角形,它的面积为
| 1 |
| 2 |
| 3 |
∴此三棱柱的体积V=S△ABC×AA1=2
| 3 |
| 3 |
故选:B.
点评:本题考查三棱柱的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
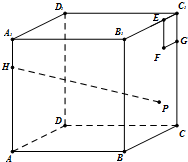 如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1棱长为4,点H在棱AA1上,且HA1=1.在侧面BCC1B1内作边长为1的正方形EFGC1,P是侧面BCC1B1内一动点,且点P到平面CDD1C1距离等于线段PF的长.则当点P运动时,|HP|2的最小值是( )| A、21 | B、22 | C、23 | D、25 |
若a=
,b=lgπ,c=e-
,则( )
| 1 |
| sin7 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<a<b |
| C、b<a<c |
| D、b<c<a |