题目内容
已知点P在椭圆
+
=1上运动，点Q、R分别在两圆（x+3）2+y2=1和（x-3）2+y2=1上运动，则|PQ|+|PR|的最小值为（ ）
| x2 |
| 16 |
| y2 |
| 7 |
| A、4 | B、6 | C、13 | D、5 |
考点：圆与圆锥曲线的综合
专题：圆锥曲线的定义、性质与方程
分析：求出椭圆的焦点坐标，恰为两圆（x+3）2+y2=1和（x-3）2+y2=1的圆心坐标，再利用三角形两边之差小于第三边，求出|PQ|、|PR|的最小值，利用椭圆的定义，即可得出结论．
解答：
解：椭圆
+
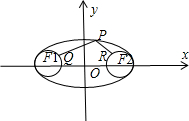
=1的两焦点为（-3，0），（3，0），恰为两圆（x+3）2+y2=1和（x-3）2+y2=1的圆心坐标．
设椭圆左右焦点为F1，F2，由三角形两边之差小于第三边知：|PQ|最小为|PF1|-1，最大为|PF1|+1．
同理：|PR|最小为|PF2|-1，最大为|PF2|+1，
∴|PQ|+|PR|的最小为|PF1|+|PF2|-2=2×4-2=6．
故选B．
解：椭圆| x2 |
| 16 |
| y2 |
| 7 |
设椭圆左右焦点为F1，F2，由三角形两边之差小于第三边知：|PQ|最小为|PF1|-1，最大为|PF1|+1．
同理：|PR|最小为|PF2|-1，最大为|PF2|+1，
∴|PQ|+|PR|的最小为|PF1|+|PF2|-2=2×4-2=6．
故选B．
点评：本题的考点是圆与圆锥曲线的综合，考查|PQ|+|PR|的最小值，正确利用椭圆的标准方程是关键．
练习册系列答案
阅读快车系列答案
相关题目
已知点E（2，1）和圆O：x2+y2=16．若A为不等式组
表示的平面区域，则当a从-1连续变化到2，动直线2x+y=a扫过A中那部分区域的面积为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
如果a＜b＜0，那么下面一定成立的是（ ）
| A、a-b＞0 | ||||
| B、ac＜bc | ||||
C、
| ||||
| D、a2＞b2 |
某同学在四次语文单元测试中，其成绩的茎叶图如图所示，则该同学语文成绩的方差