题目内容
某软件公司研发了多款软件,其中A,B,C三种软件供高中生使用,经某高中使用一学年后,该公司调查了这个学校同一年级四个班的使用情况,从各班抽取的样本人数如下表:
(1)从这12人中随机抽取2人,求这2人恰好来自同一个班级的概率;
(2)从这12人中,指定甲、乙、丙3人为代表,已知他们每人选择一款软件,其中选A,B两款软件的概率都是
,且他们选择A,B,C任一款软件都是相互独立的.设这3名学生中选择软件C的人数为ξ,求ξ的分布列和数学期望.
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12人中,指定甲、乙、丙3人为代表,已知他们每人选择一款软件,其中选A,B两款软件的概率都是
| 1 |
| 6 |
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用互斥事件的概率公式能求出从这12人中随机抽取2人,求这2人恰好来自同一个班级的概率.
(2)每个人选软件C的概率均为
,由题意知ξ=0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
(2)每个人选软件C的概率均为
| 2 |
| 3 |
解答:
解:(1)设“从这12人中随机抽取2人,求这2人恰好来自同一个班级”为事件M,
则P(M)=
=
(4分)
(2)由题意知ξ=0,1,2,3,每个人选软件C的概率均为
,
P(ξ=0)=(
)3=
,
P(ξ=1)=
(
)2
=
,
P(ξ=2)=
(
)2=
,
P(ξ=3)=(
)3=
,(10分)
∴ξ的分布列如下:
E(ξ)=0×
+1×
+2×
+3×
=2.(14分)
则P(M)=
| ||||||||
|
| 13 |
| 66 |
(2)由题意知ξ=0,1,2,3,每个人选软件C的概率均为
| 2 |
| 3 |
P(ξ=0)=(
| 1 |
| 3 |
| 1 |
| 27 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(ξ=3)=(
| 2 |
| 3 |
| 8 |
| 27 |
∴ξ的分布列如下:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
等差数列{an},前n项和为Sn,a1>0,a2012,a2013是方程x2-(λ2+λ+1)x-(λ2+1)=0的两根,则满足Sn>0的n的最大正整数为( )
| A、4023 | B、4024 |
| C、4025 | D、4026 |
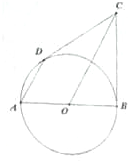 如图,AB为圆O的直径,BC与圆O相切于点B,D为圆O上的一点,AD∥OC,连接CD.
如图,AB为圆O的直径,BC与圆O相切于点B,D为圆O上的一点,AD∥OC,连接CD.