题目内容
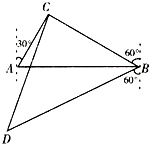某海域设立东西方向两个观测点A、B，相距20
| ||
| 3 |
考点：解三角形的实际应用
专题：解三角形
分析：先根据题意求得BC，进而在△BCD中，根据余弦定理求得DC，进而根据里程和速度即可求得时间．
解答：
解：如图：由题意知△ABC为直角三角形，∠ACB=90°，
AB=
，
∴BC=ABcos30°=10，
又∵BD=16，∠CBD=60°，
在△BCD中，根据余弦定理得：
DC2=BC2+BD2-2BC•BD cos60°=102+162-2×10×16×
=196，
∴DC=14（海里），则需要的时间为 t=
=0.5小时．
解：如图：由题意知△ABC为直角三角形，∠ACB=90°，AB=
20
| ||
| 3 |
∴BC=ABcos30°=10，
又∵BD=16，∠CBD=60°，
在△BCD中，根据余弦定理得：
DC2=BC2+BD2-2BC•BD cos60°=102+162-2×10×16×
| 1 |
| 2 |
∴DC=14（海里），则需要的时间为 t=
| DC |
| 28 |
点评：本题主要考查了解三角形的实际应用．解题的关键时把实际问题转化成解三角形的问题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，sinC=2sinAcosB，则△ABC的形状为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、不能确定 |
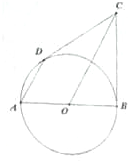如图，AB为圆O的直径，BC与圆O相切于点B，D为圆O上的一点，AD∥OC，连接CD．
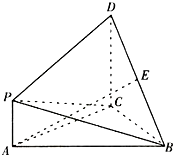如图，△ABC是等边三角形，PA⊥平面ABC，DC∥PA，且DC=AC=2PA=2，E是BD的中点．