题目内容
若A={x|x2+x+a=0,B={x|x<0},已知A⊆B,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:由A={x|x2+x+a=0,B={x|x<0},A⊆B,可得A=∅或x2+x+a=0有两个相等负实数根或两个不相等负实数根.解出即可.
解答:
解:∵A={x|x2+x+a=0,B={x|x<0},A⊆B,
∴A=∅或x2+x+a=0有两个相等负实数根或两个不相等负实数根.
①A=∅时,△<0,∴1-4a<0,解得a>
.
②x2+x+a=0有两个相等负实数根,△=0,∴1-4a=0,解得a=
.
③x2+x+a=0有两个不相等负实数根,则
,解得0<a<
.
综上可得:实数a的取值范围是a>0.
∴A=∅或x2+x+a=0有两个相等负实数根或两个不相等负实数根.
①A=∅时,△<0,∴1-4a<0,解得a>
| 1 |
| 4 |
②x2+x+a=0有两个相等负实数根,△=0,∴1-4a=0,解得a=
| 1 |
| 4 |
③x2+x+a=0有两个不相等负实数根,则
|
| 1 |
| 4 |
综上可得:实数a的取值范围是a>0.
点评:本题考查了集合之间的关系、一元二次方程的实数根与判别式之间的关系,考查了分类讨论的思想方法,属于中档题.

练习册系列答案
相关题目
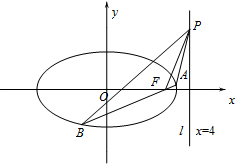 如图:椭圆C:
如图:椭圆C: 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M、N分别在AC、PB上,且AM=
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M、N分别在AC、PB上,且AM=