题目内容
设定义在[-2,2]上的奇函数f(x)在区间[-2,2]上单调递减,若f(1-m)+f(-m)<0,求实数m的取值范围.
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:据函数为定义在[-2,2]上的奇函数,将已知不等式移项整理可得f(1-m)<f(m).再由f(x)在[-2,2]上是减函数,由此建立关于m的不等式组并解之,即可得到实数m的取值范围.
解答:
解:由(1-m)+f(-m)<0,移项得(1-m)<-f(-m),
∵f(x)是定义在[-2,2]上的奇函数
∴-f(-m)=f(m),不等式化成f(1-m)<f(m).?
又∵f(x)在[-2,2]上为减函数.(6分)
∴,
,解之得-1≤m<0.5
综上所述,可得m的取值范围为[-1,0.5).?
∵f(x)是定义在[-2,2]上的奇函数
∴-f(-m)=f(m),不等式化成f(1-m)<f(m).?
又∵f(x)在[-2,2]上为减函数.(6分)
∴,
|
综上所述,可得m的取值范围为[-1,0.5).?
点评:本题给出抽象函数的单调性和奇偶性,求解关于m的不等式,着重考查了函数的单调性、奇偶性和抽象函数的理解等知识,属于基础题.

练习册系列答案
相关题目
若函数f(x)=-a•2x与f(x)=4x+a+1的图象有交点,则a的取值范围是( )
A、a≤2-2
| ||||
| B、a<-1 | ||||
C、-1≤a≤2-2
| ||||
D、a≤2-2
|
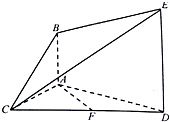 如图所示,AB∥平面ACD,DE∥AB,△ACD是正三角形,F是CD的中点,AD=4,DE=2AB=3.
如图所示,AB∥平面ACD,DE∥AB,△ACD是正三角形,F是CD的中点,AD=4,DE=2AB=3.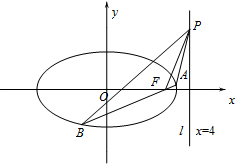 如图:椭圆C:
如图:椭圆C: