题目内容
已知方程ax2+2x+c=0（a、c∈N+）有实数根．
（1）求f（x）=ax2+2x+c的解析式；
（2）若x∈[-2，2]，求函数f（x）的值域．
（1）求f（x）=ax2+2x+c的解析式；
（2）若x∈[-2，2]，求函数f（x）的值域．
考点：函数解析式的求解及常用方法,函数的值域
专题：函数的性质及应用
分析：（1）由题意得到△=4-4ac≥0，即ac≤1，再根据a、c∈N+求出ac的值，代入即可．
（2）利用配方法求最值，问题得以解决．
（2）利用配方法求最值，问题得以解决．
解答：
解：（1）∵方程ax2+2x+c=0（a、c∈N+）有实数根．
∴△=4-4ac≥0，
∴ac≤1，
∴a=c=1，
∴f（x）=x2+2x+1，
（2）∵f（x）=x2+2x+1=（x+1）2，
∴当x=-1∈[-2，2]有最小值，最小值为0，
当x=2有最大值，最大值为9，
∴函数f（x）的值域为[0，9]
∴△=4-4ac≥0，
∴ac≤1，
∴a=c=1，
∴f（x）=x2+2x+1，
（2）∵f（x）=x2+2x+1=（x+1）2，
∴当x=-1∈[-2，2]有最小值，最小值为0，
当x=2有最大值，最大值为9，
∴函数f（x）的值域为[0，9]
点评：本题主要考查了函数解析式的求法和函数值域的求法，属于基础题．
练习册系列答案
相关题目
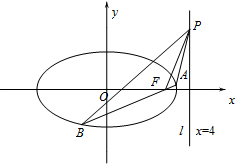如图：椭圆C：