题目内容
函数y-ex在x=0处的切线方程为（ ）
| A、y=x | B、y=0 |
| C、y=2x | D、y=x+1 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出函数的导函数，把x=0代入导函数求出的函数值即为切线方程的斜率，把x=0代入函数解析式中得到切点的纵坐标，进而确定出切点坐标，根据求出的斜率和切点坐标写出切线方程即可．
解答：
解：由题意得：y′=ex，把x=0代入得：y′|x=0=1，即切线方程的斜率k=1，
且把x=0代入函数解析式得：y=1，即切点坐标为（0，1），
则所求切线方程为：y-1=x，即y=x+1．
故选D．
且把x=0代入函数解析式得：y=1，即切点坐标为（0，1），
则所求切线方程为：y-1=x，即y=x+1．
故选D．
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，考查运算能力，是一道基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
储油30m3的油桶，每分钟流出
m3的油，则桶内剩余油量Q（m3）以流出时间t（分）为自变量的函数的定义域为（ ）
| 3 |
| 4 |
| A、[0，+∞） | ||
B、[0，
| ||
| C、（-∞，40] | ||
| D、[0，40] |
已知椭圆C：
+
=1（b＞0）的左、右焦点分别为F1，F2，直线AB过右焦点F2，和椭圆C交于A，B两点，且满足
=2
，∠F1AB=90°，则椭圆C的离心率为（ ）
| x2 |
| 3 |
| y2 |
| b2 |
| AF1 |
| F2B |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
阅读如图所示的程序框图，若输入m=5，n=3，则输出a，i分别是（ ）
| A、a=15，i=3 |
| B、a=15，i=5 |
| C、a=10，i=3 |
| D、a=8，i=4 |
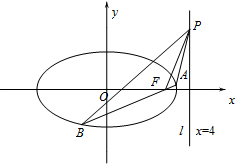如图：椭圆C：