题目内容
有一个圆锥的侧面展开图是一个半径为5、圆心角为
的扇形,在这个圆锥中内接一个高为x的圆柱.
(1)求圆锥的体积;
(2)当x为何值时,圆柱的侧面积最大?
| 6π |
| 5 |
(1)求圆锥的体积;
(2)当x为何值时,圆柱的侧面积最大?
考点:旋转体(圆柱、圆锥、圆台)
专题:综合题,空间位置关系与距离
分析:(1)利用侧面展开图中心角公式求得圆锥的底面圆半径,再利用勾股定理求得圆锥的高,代入圆锥的体积公式计算;
(2)根据轴截面图,设圆柱的底面半径为R,可得
=
,求出内接圆柱的底面圆半径,计算圆柱的侧面积,利用基本不等式,即可得出结论.
(2)根据轴截面图,设圆柱的底面半径为R,可得
| 3-R |
| 3 |
| x |
| 4 |
解答:
解:(1)∵圆锥侧面展开图的半径为5,
∴圆锥的母线长为5.
设圆锥的底面半径为r,
则2πr=
,解得r=3,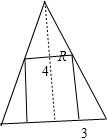
∴圆锥的高为4.
∴圆锥的体积V=
π×32×4=12π;
(2)设圆柱的底面半径为R,则
=
,∴R=3-
x,
∴圆柱的侧面积为2π(3-
x)x=
π(4-x)x≤
π×(
)2=6π,
当且仅当4-x=x,即x=2时,圆柱的侧面积最大.
∴圆锥的母线长为5.
设圆锥的底面半径为r,
则2πr=
| 216×π×5 |
| 180 |

∴圆锥的高为4.
∴圆锥的体积V=
| 1 |
| 3 |
(2)设圆柱的底面半径为R,则
| 3-R |
| 3 |
| x |
| 4 |
| 3 |
| 4 |
∴圆柱的侧面积为2π(3-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 4-x+x |
| 2 |
当且仅当4-x=x,即x=2时,圆柱的侧面积最大.
点评:本题考查了圆锥的侧面展开图及侧面展开图中心角公式,考查了圆锥与圆柱的体积公式,解题的关键是利用比例关系求得内接圆柱的底面圆半径.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
阅读如图所示的程序框图,若输入m=5,n=3,则输出a,i分别是( )


| A、a=15,i=3 |
| B、a=15,i=5 |
| C、a=10,i=3 |
| D、a=8,i=4 |
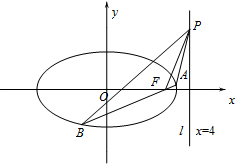 如图:椭圆C:
如图:椭圆C: