题目内容
18．若i为虚数单位，设复数z满足|z|=1，则|z-1+i|的最大值为（ ）| A． | $\sqrt{2}$-1 | B． | 2-$\sqrt{2}$ | C． | $\sqrt{2}$+1 | D． | 2+$\sqrt{2}$ |
分析 由题意画出图形，再由|z-1+i|=|z-（1-i）|的几何意义，即动点Z到定点P（1，-1）的距离求解．
解答 解：|z-1+i|=|z-（1-i）|，其几何意义为动点Z到定点P（1，-1）的距离，
又|z|=1，如图：
则|z-1+i|的最大值为$\sqrt{2}+1$．
故选：C．
点评 本题考查复数模的求法，考查数形结合的解题思想方法，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，
9．
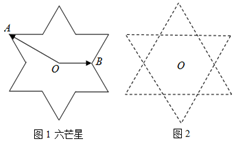如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（ ）
如图2，“六芒星”是由两个全等正三角形组成，中心重合于点O且三组对边分别平行．点A，B是“六芒星”（如图1）的两个顶点，动点P在“六芒星”上（内部以及边界），若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$，则x+y的取值范围是（ ）| A． | [-4，4] | B． | $[{-\sqrt{21}，\sqrt{21}}]$ | C． | [-5，5] | D． | [-6，6] |
3．设a＞0，b＞0，则“a＞b”是“lna＞lnb”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 既不充分也不必要条件 | D． | 充要条件 |
7．已知方程2x2-（m+1）x+m=0有两个不等正实根，则实数m的取值范围是（ ）
| A． | $0＜m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ | B． | $m＜3-2\sqrt{2}$或$m＞3+2\sqrt{2}$ | ||
| C． | $0＜m＜3-2\sqrt{2}$或$m＞3+2\sqrt{2}$ | D． | $m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ |