题目内容
1．若复数z满足i•z=$\frac{1}{2}$（1+i），则z的虚部是（ ）| A． | -$\frac{1}{2}$i | B． | $\frac{1}{2}$i | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 把已知等式变形，然后利用复数代数形式的乘除运算化简得答案．
解答 解：由i•z=$\frac{1}{2}$（1+i），得$z=\frac{1+i}{2i}=\frac{（1+i）（-i）}{-2{i}^{2}}=\frac{1}{2}-\frac{i}{2}$，
∴z的虚部为$-\frac{1}{2}$．
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
12．在平面直角坐标系xoy中，双曲线的中心在原点，焦点在y轴上，一条渐近线与直线2x+y-1=0垂直，则双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
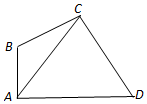如图，在平面四边形ABCD中，AB⊥AD，AB=1，AC=$\sqrt{7}$，△ABC的面积S△ABC=$\frac{{\sqrt{3}}}{2}$，DC=$\frac{{4\sqrt{7}}}{5}$