题目内容
1.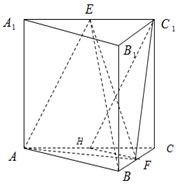 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.(1)求证:平面C1HF∥平面ABE.
(2)求证:平面AEF⊥平面B1BCC1.
分析 (1)证明HF∥AB.EC1∥AH,推出C1H∥AE,然后证明平面C1HF∥平面ABE.
(2)证明AF⊥BC,B1B⊥AF,得到AF⊥平面B1BCC1,然后证明平面AEF⊥平面B1BCC1
解答 (本小题8分)证明:(1)∵F,H分别是BC,AC的中点,∴HF∥AB.
又∵E,H分别是A1C1,AC的中点,∴EC1∥AH
又∵EC1=AH∴四边形EC1HA为平行四边形.∴C1H∥AE,
又∵C1H∩HF=H,AE∩AB=A,
所以平面C1HF∥平面ABE.
(2)∵AB=AC,F为BC中点,∴AF⊥BC,∵B1B⊥平面ABC,AF?平面ABC,
∴B1B⊥AF,∵B1B∩BC=B,∴AF⊥平面B1BCC1
又∵AF?平面AEF,
∴平面AEF⊥平面B1BCC1
点评 本题考查平面与平面垂直以及平面与平面平行的判定定理的应用,考查空间想象能力以及逻辑推理能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
12.已知锐角α终边上一点A的坐标为(2sin3,-2cos3),则角α的弧度数为( )
| A. | 3 | B. | π-3 | C. | 3-$\frac{π}{2}$ | D. | $\frac{π}{2}$-3 |
13.若$α∈(0,\frac{π}{2})$,且${sin^2}α+cos2α=\frac{1}{4}$,则tanα的值等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
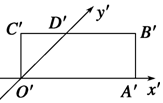 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )