题目内容
8.若直线y=2x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)有公共点,则双曲线的离心率的取值范围为( )| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,+∞) | C. | (1,$\sqrt{5}$] | D. | [$\sqrt{5}$,+∞) |
分析 求得双曲线的渐近线方程,由双曲线与直线y=2x有交点,应有渐近线的斜率$\frac{b}{a}$>2,再由离心率e=$\frac{c}{a}$═$\sqrt{1+(\frac{b}{a})^{2}}$,可得e的范围.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
由双曲线与直线y=2x有交点,
则有$\frac{b}{a}$>2,
即有e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+(\frac{b}{a})^{2}}$>$\sqrt{1+4}$=$\sqrt{5}$,
则双曲线的离心率的取值范围为($\sqrt{5}$,+∞).
故选:B.
点评 本题考查了双曲线的方程和性质,主要是渐近线和离心率,直线与双曲线相交等问题,属于中档题.

练习册系列答案
相关题目
13.若$α∈(0,\frac{π}{2})$,且${sin^2}α+cos2α=\frac{1}{4}$,则tanα的值等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
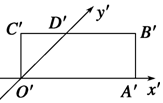 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )