题目内容
5.设常数a∈R,函数f(x)=|x-1|+|x2-a|,若f(2)=1,则a=4.分析 根据已知中函数f(x)=|x-1|+|x2-a|,将x=2代入构造方程,解得答案.
解答 解:∵函数f(x)=|x-1|+|x2-a|,
∴f(2)=|2-1|+|4-a|=1+|4-a|=1,
∴|4-a|=0,
解得:a=4,
故答案为:4.
点评 本题考查的知识点是绝对值的定义,分段函数的应用,函数求值,难度中档.

练习册系列答案
相关题目
13.若$α∈(0,\frac{π}{2})$,且${sin^2}α+cos2α=\frac{1}{4}$,则tanα的值等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
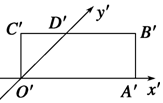 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )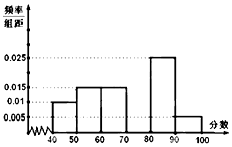 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: