题目内容
已知平面直角坐标系中，点O为原点，A（-3，-4），B（5，-12），若
=
+
，
=
-
．
（Ⅰ）求点C和点D的坐标；
（Ⅱ）求
•
．
| OC |
| OA |
| OB |
| OD |
| OA |
| OB |
（Ⅰ）求点C和点D的坐标；
（Ⅱ）求
| OC |
| OD |
考点：向量加减混合运算及其几何意义,平面向量的坐标运算
专题：计算题,平面向量及应用
分析：（Ⅰ）求出向量
、
，即得点C、D的坐标；
（Ⅱ）由向量
、
直接求出它们的数量积．
| OC |
| OD |
（Ⅱ）由向量
| OC |
| OD |
解答：
解：（Ⅰ）∵
=（-3，-4），
=（5，-12），
∴
=
+
=（-3+5，-4-12）=（2，-16），
=
-
=（-3-5，-4+12）=（-8，8）；
∴点C（2，-16），点D（-8，8）；
（Ⅱ）
•
=2×（-8）+（-16）×8=-144．
| OA |
| OB |
∴
| OC |
| OA |
| OB |
| OD |
| OA |
| OB |
∴点C（2，-16），点D（-8，8）；
（Ⅱ）
| OC |
| OD |
点评：本题考查了平面向量的运算问题，解题时应根据平面向量的运算法则进行计算即可，是基础题．
练习册系列答案
相关题目
将一枚骰子连续抛掷两次，则向上点数之差的绝对值不大于3的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
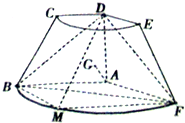如图，在直角梯形ABCD中，AB=AD=2，把此梯形绕其直角边AD旋转120°得到如图所示的几何体，点G是∠BDF平分线上任意一点（异于点D），点M是弧
如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起到△APM，使得平面APM⊥平面ABCM，点E在线段PB上，且PE=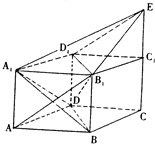
如图，已知直四棱柱ABCD-A1B1C1D1中，AB=AA1，底面ABCD为菱形，∠ADC=120°，E为CC1延长线上一点．