题目内容
数列{an}满足a1+2a2+22a3+…+2n-1an=
(n∈N*)前n项和为Sn;数列{bn}是等差数列,且b1=2,其前n项和Tn满足Tn=nλ•bn+1(λ为常数,且λ<1).
(1)求数列{an}的通项公式及λ的值;
(2)设cn=
,求数列{cn}的前n项的和Pn.
| n |
| 2 |
(1)求数列{an}的通项公式及λ的值;
(2)设cn=
| n |
| an |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由a1+2 a2+22 a3+…+2n-1an=
,得a1+2 a2+22 a3+…+2n-2 an-1=
,两式相减得an=
;由已知条件得
,且λ<1,解得λ=
.
(2)由Cn=n•2n,利用错位相减法能求出数列{cn}的前n项的和Pn.
| n |
| 2 |
| n-1 |
| 2 |
| 1 |
| 2n |
|
| 1 |
| 2 |
(2)由Cn=n•2n,利用错位相减法能求出数列{cn}的前n项的和Pn.
解答:
解:(1)∵a1+2 a2+22 a3+…+2n-1an=
,①
∴a1+2 a2+22 a3+…+2n-2 an-1=
(n≥2),②
①-②得2n-1 an=
-
=
(n≥2),化简得an=
(n≥2).
n=1时也满足上式,故an=
(n∈N*).
由于{bn}成等差,且b1=2,
设公差为d,则
,
解得
或
又λ<1,∴
,∴bn=2n,
∴
,an=
(n∈N*),
∴an=
,λ=
.
(2)∵Cn=n•2n,
∴pn=1•2+2•22+3•23+…+n•2n,③
2pn=1•22+2•23+3•24+…+n•2n+1,④
③-④得-pn=2+22+23+…+2n-n•2n+1,
∴pn=(1-n)2n+1-2.
| n |
| 2 |
∴a1+2 a2+22 a3+…+2n-2 an-1=
| n-1 |
| 2 |
①-②得2n-1 an=
| n |
| 2 |
| n-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
n=1时也满足上式,故an=
| 1 |
| 2n |
由于{bn}成等差,且b1=2,
设公差为d,则
|
解得
|
|
又λ<1,∴
|
∴
|
| 1 |
| 2n |
∴an=
| 1 |
| 2n |
| 1 |
| 2 |
(2)∵Cn=n•2n,
∴pn=1•2+2•22+3•23+…+n•2n,③
2pn=1•22+2•23+3•24+…+n•2n+1,④
③-④得-pn=2+22+23+…+2n-n•2n+1,
∴pn=(1-n)2n+1-2.
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错痊相减法的合理运用.

练习册系列答案
相关题目
sin30°=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
 某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )| A、11小时 | B、13小时 |
| C、15小时 | D、10小时 |
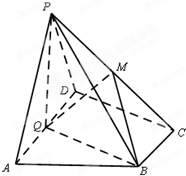 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=