题目内容
 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=| 1 |
| 3 |
(Ⅰ)求证:AP⊥BM;
(Ⅱ)求三棱锥ABEM的体积.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)先证明BM⊥AM,再利用平面ADM⊥平面ABCM,证明BM⊥平面ADM,从而可得AD⊥BM;
(Ⅱ)取AM的中点N,连接PN,NB,在NB上取点F,使NF=
NB,连接EF,证明EF⊥平面ABM,EF=
,即可求三棱锥ABEM的体积.
(Ⅱ)取AM的中点N,连接PN,NB,在NB上取点F,使NF=
| 1 |
| 3 |
| ||
| 3 |
解答:
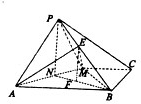 (Ⅰ)证明:∵长方形ABCD中,AB=2,AD=1,M为DC的中点,
(Ⅰ)证明:∵长方形ABCD中,AB=2,AD=1,M为DC的中点,
∴AM=BM=
,
∴AB2=AM2+BM2,
∴BM⊥AM,
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM
∴BM⊥平面ADM
∵AD?平面ADM
∴AD⊥BM;
(Ⅱ)解:取AM的中点N,连接PN,NB,则PN⊥平面ABM,且PN=
,
在NB上取点F,使NF=
NB,连接EF,
∵PE=
PB,
∴EF∥PN,
∴EF⊥平面ABM,EF=
.
∵S△ABM=
×
×
=1,
∴VA-BEM=VE-ABM=
×1×
=
.
 (Ⅰ)证明:∵长方形ABCD中,AB=2,AD=1,M为DC的中点,
(Ⅰ)证明:∵长方形ABCD中,AB=2,AD=1,M为DC的中点,∴AM=BM=
| 2 |
∴AB2=AM2+BM2,
∴BM⊥AM,
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM?平面ABCM
∴BM⊥平面ADM
∵AD?平面ADM
∴AD⊥BM;
(Ⅱ)解:取AM的中点N,连接PN,NB,则PN⊥平面ABM,且PN=
| ||
| 2 |
在NB上取点F,使NF=
| 1 |
| 3 |
∵PE=
| 1 |
| 3 |
∴EF∥PN,
∴EF⊥平面ABM,EF=
| ||
| 3 |
∵S△ABM=
| 1 |
| 2 |
| 2 |
| 2 |
∴VA-BEM=VE-ABM=
| 1 |
| 3 |
| ||
| 3 |
| ||
| 9 |
点评:本题考查线面垂直,考查三棱锥ABEM的体积,正确运用面面垂直的性质,掌握线面垂直的判定方法是关键.

练习册系列答案
相关题目
正方体ABCD-A′B′C′D′中,向量
与
的夹角是( )
| AB′ |
| BC′ |
| A、30° | B、45° |
| C、60° | D、90° |
复数
+2等于( )
| (1+i)4 |
| 1-i |
| A、2-2i | B、-2i |
| C、1-i | D、2i |
一个口袋内有大小、形状相同的6个白球和5个黑球,从中随机取出3个球,则至少取到2个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
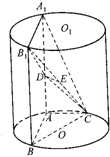 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,AB=AC.