题目内容
设函数f（x）=x3-x2，则f′（1）的值为（ ）
| A、-1 | B、0 | C、1 | D、5 |
考点：导数的运算
专题：导数的概念及应用
分析：求函数的导数，直接代入即可得到结论．
解答：
解：∵f（x）=x3-x2，
∴f′（x）=3x2-2x，
则f′（1）=3-2=1，
故选：C．
∴f′（x）=3x2-2x，
则f′（1）=3-2=1，
故选：C．
点评：本题主要考查函数值的计算，利用导数公式是解决本题的关键，比较基础．
练习册系列答案
相关题目
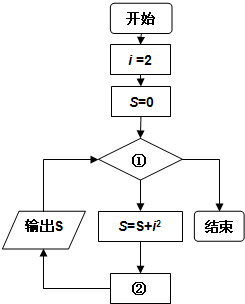如图是表示输出22，22+42，22+42+62，…，22+42+62+…+20042的值的过程的一个程序框图，那么在图中①、②处应分别填上（ ）| A、i≤2014，i=i+2 |
| B、i≤1007，i=i+2 |
| C、i≤2014，i=i+1 |
| D、i≤1007，i=i+1 |
设集合M={x|2x＜
}，N={x|-2≤x≤3}，则M∩N=（ ）
| 1 |
| 2 |
| A、[-2，1） |
| B、[-2，-l） |
| C、（-1，3] |
| D、[-2，3] |
如果
+
=1表示焦点在x轴上的椭圆，则实数a的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| a+2 |
| A、（-2，+∞） |
| B、（-2，-1）∪（2，+∞） |
| C、（-∞，-1）∪（2，+∞） |
| D、任意实数R |
直线3x-y+1=0的斜率是（ ）
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
若不等式ax2+ax-1＜0对一切x∈R恒成立，则实数a的取值范围是（ ）
| A、（-∞，0） |
| B、（-∞，0] |
| C、（-4，0） |
| D、（-4，0] |
已知一几何体三视图如图，则其体积为（ ）
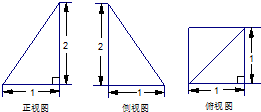
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
