题目内容
下列函数中，既是奇函数又是（-1，1）上的增函数的是（ ）
| A、y=2x |
| B、y=tanx |
| C、y=x-1 |
| D、y=cosx |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：根据题意，对选项中的基本初等函数的奇偶性与单调性进行判断即可．
解答：
解：对于A，y=2x，在定义域R上是非奇非偶的函数，∴不满足条件；
对于B，y=tanx是定义域（-
+kπ，
+kπ），k∈Z上的奇函数，且在每一个区间上是增函数，∴满足题意；
对于C，y=x-1，在区间（-∞，0）和（0，+∞）上是减函数，∴不满足题意；
对于D，y=cosx，在区间[2kπ，π+2kπ]，k∈Z上是减函数，∴在（-1，1）上是减函数，不满足条件．
故选：B．
对于B，y=tanx是定义域（-
| π |
| 2 |
| π |
| 2 |
对于C，y=x-1，在区间（-∞，0）和（0，+∞）上是减函数，∴不满足题意；
对于D，y=cosx，在区间[2kπ，π+2kπ]，k∈Z上是减函数，∴在（-1，1）上是减函数，不满足条件．
故选：B．
点评：本题考查了基本初等函数的奇偶性与单调性的判断问题，是基础题目．
练习册系列答案
相关题目
已知函数f（x）=2如图所示的程序框图是给出计算
+
+
+…+
的值，则判断框内应填入的条件是（ ）
| 1 |
| 5 |
| 1 |
| 10 |
| 1 |
| 15 |
| 1 |
| 2015 |
| A、i≤403？ |
| B、i＜403？ |
| C、i≤404？ |
| D、i＞404？ |
将函数f（x）=sin（2x+φ）（|φ|＜
）的图象向左平移
个单位后的图形关于原点对称，则函数f（x）在[0，
]上的最小值为（ ）
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
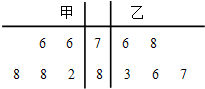甲、乙两名同学在5次体能测试中的成绩的茎叶图如图所示，设. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设A、B、C是三角形的三个内角，下列关系恒成立的是（ ）
| A、sin（A+B）=sinC | ||||
| B、cos（A+B）=cosC | ||||
| C、tan（A+B）=tanC | ||||
D、sin
|
已知集合 A={2，-2}，B={x|x2-ax+4=0}，若A∪B=A，则实数a满足（ ）
| A、{a|-4＜a＜4} |
| B、{a|-2＜a＜2} |
| C、{-4，4} |
| D、{a|-4≤a≤4} |