题目内容
6．已知双曲线${x^2}-\frac{y^2}{b^2}=1\;（b＞0）$的一个焦点是（2，0），则其渐近线的方程为（ ）| A． | $\sqrt{3}x±y=0$ | B． | 3x±y=0 | C． | $x±\sqrt{3}y=0$ | D． | x±3y=0 |
分析 利用双曲线的焦点坐标求出c，然后求解b，即可求解双曲线的渐近线方程．
解答 解：双曲线${x^2}-\frac{y^2}{b^2}=1\;（b＞0）$的一个焦点是（2，0），
可得1+b2=4，解得b=$\sqrt{3}$．
双曲线${x}^{2}-\frac{{y}^{2}}{3}=1$ 则其渐近线的方程为：$\sqrt{3}x±y=0$．
故选：A．
点评 本题考查双曲线的简单性质的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
1．若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一个焦点是圆x2+y2-10x+24=0的圆心，且虚轴长为6，则双曲线的离心率为（ ）
| A． | $\frac{5}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{4}{3}$ | D． | $\sqrt{2}$ |
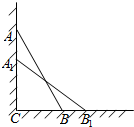如图，一根木棒AB长为2米，斜靠在墙壁AC上，∠ABC=60°，若AB滑动至A1B1位置，且$A{A_1}=（\sqrt{3}-\sqrt{2}）$米，则①BB1=$\sqrt{2}$-1米；②木棒AB的中点D所经过的路程为$\frac{π}{12}$米．