题目内容
11.已知圆C的参数方程为$\left\{{\begin{array}{l}{x=2+3cosθ}\\{y=3sinθ-2}\end{array}}\right.(θ为参数)$,以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsinθ+2ρcosθ=3,求直线l被圆C截得的弦长.分析 先求出圆和直线的直角坐标方程,再求出圆心C(2,-2)到直线l的距离d和圆半径r,利用勾股定理能求出直线l被圆C截得的弦长.
解答 解:∵圆C的参数方程为$\left\{{\begin{array}{l}{x=2+3cosθ}\\{y=3sinθ-2}\end{array}}\right.(θ为参数)$,
∴圆C的直角坐标方程为(x-2)2+(y+2)2=9,
∵直线l的极坐标方程为ρsinθ+2ρcosθ=3,
∴直线l的直角坐标方程为2x+y=3,
∵圆心C(2,-2)到直线l的距离d=$\frac{|2×2-2-3|}{\sqrt{4+1}}$=$\frac{\sqrt{5}}{5}$,圆半径r=3,
∴直线l被圆C截得的弦长|AB|=2$\sqrt{{3}^{2}-(\frac{\sqrt{5}}{5})^{2}}$=$\frac{4\sqrt{55}}{5}$.
点评 本题考查直线被圆截得的弦长的求法,是基础题,解题时要认真审题,注意直角坐标和极坐标互化公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知双曲线${x^2}-\frac{y^2}{b^2}=1\;(b>0)$的一个焦点是(2,0),则其渐近线的方程为( )
| A. | $\sqrt{3}x±y=0$ | B. | 3x±y=0 | C. | $x±\sqrt{3}y=0$ | D. | x±3y=0 |
 如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.
如图,在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连结BC1,过B1作B1E⊥BC1交CC1于点E.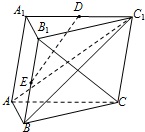 如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证:
如图,在三棱柱ABC-A1B1C1中,D,E分别为A1C1,BB1的中点,B1C⊥AB,侧面BCC1B1为菱形.求证: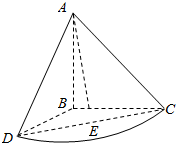 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求: