题目内容
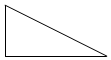
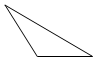
13.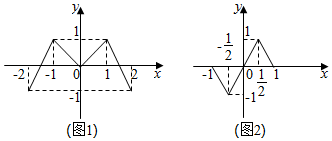 已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
已知偶函数f(x),奇函数g(x)的图象分别如图(1)、图(2)所示,若f(y0)=0且y0=g(x0),则x0的值为-1,0,或1.
分析 根据g(x)的图象便可得到-1≤y0≤1,而由f(x)的图象及f(y0)=0便可得出y0=0,从而便可由g(x)的图象和g(x0)=0即可解出x0的值.
解答 解:根据g(x)的图象得,-1≤y0≤1;
∴由f(x)的图象及f(y0)=0得,y0=0;
∴g(x0)=0;
∴x0=-1,0,或1.
故答案为:-1,0,或1.
点评 考查根据函数图象求函数值域的方法,以及根据函数图象求函数零点的方法,求函数零点时要注意自变量的范围.

练习册系列答案
相关题目
1.某校高三数学备课组为了更好的制定二轮复习的计划,开展了试卷讲评后效果的调研,从上学期期末数学试题中选出一些学生易错题.重新进行测试,并认为做这些题不出任何错误的同学为“过关”,出了错误的同学认为“不过关”,现随机调查了年级50人,他们的测试成绩的频数分别如表:
(1)由以上统计数据完成如下2×2列联表,并判断是否有95%的把认为期末数学成绩不低于90分与测试“过关”有关?说明你的理由.
(2)在期末分数段[105,120)的5人中,从中随机选3人,记抽取到过关测试“过关”的人数为X,求X的分布列及数学期望.
下面的临界值表供参考:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 期末分数段 | (0,60) | [60,75) | [75,90) | [90,105) | [105,120) | [120,150] |
| 人数 | 5 | 10 | 15 | 10 | 5 | 5 |
| “过关”人数 | 1 | 2 | 9 | 7 | 3 | 4 |
| 分数低于90分人数 | 分数不低于90分人数 | 合计 | |
| 过关人数 | |||
| 不过关人数 | |||
| 合计 |
下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 |
| K | 2.072 | 2.706 | 3.841 | 5.024 |
18.已知a∈R,则a=1是复数$z=\frac{1+ai}{1-ai}$(i为虚数单位)为纯虚数的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
2.2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
乙电商:
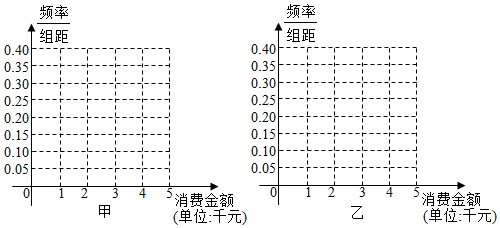
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
甲电商:
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 50 | 200 | 350 | 300 | 100 |
| 消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
| 频数 | 250 | 300 | 150 | 100 | 200 |

(Ⅱ)运用分层抽样分别从甲、乙1000名消费者中各自抽出20人放在一起,在抽出的40人中,从消费金额不小于4千元的人中任取2人,求这2人恰好是来自不同电商消费者的概率.
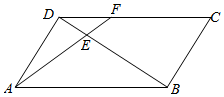 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.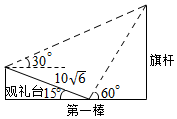 如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.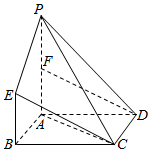 如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.
如图,矩形ABCD中,BC=2,AB=1,PA⊥平面ABCD,BE∥PA,BE=$\frac{1}{2}$PA,F为PA的中点.