题目内容
过点P(2,0)作直线l交椭圆
+y2=1于不同两点A,B,设G为线段AB的中点,直线OG交于C,D.
(1)若点G的横坐标为
,求l的方程;
(2)设△ABD与△ABC的面积分别为S1,S2,求|S1-S2|.
| x2 |
| 2 |
(1)若点G的横坐标为
| 2 |
| 3 |
(2)设△ABD与△ABC的面积分别为S1,S2,求|S1-S2|.
考点:直线与圆锥曲线的关系,直线的一般式方程
专题:圆锥曲线的定义、性质与方程
分析:(1)直线为y=k(x-2)与椭圆
+y2=1方程联立,得到
(1+2k2)x2-8k2x+8k2-2=0①运用两根与方程的系数关系求解得k的值,最后运用点的坐标求出直线方程.
(2)先求出|AB|长,OG方程,C,D坐标,再求出到直线AB的距离,用面积公式求即可.,
| x2 |
| 2 |
(1+2k2)x2-8k2x+8k2-2=0①运用两根与方程的系数关系求解得k的值,最后运用点的坐标求出直线方程.
(2)先求出|AB|长,OG方程,C,D坐标,再求出到直线AB的距离,用面积公式求即可.,
解答:
解:(1)设直线为y=k(x-2)与椭圆
+y2=1方程联立,
得到:(1+2k2)x2-8k2x+8k2-2=0①
又因为若点G的横坐标为
,G为线段AB的中点
所以:x1+x2=
=
,k2=
,即k=±
,
x1x2=
,|AB|=×
|x1-x2|
所以l的方程:y=±
(x-2)
(2)把k2=
代入①得3x2-4x=0,即x=0或x=
,
∵过点P(2,0)作直线l交椭圆
+y2=1于不同两点A,B,设G为线段AB的中点,直线OG交于C,D.
∴根据韦达定理,弦长公式;知x1x2=
,|AB|=×
|x1-x2|
所以|AB|=×
|x1-x2|=
×
=
,
当k=-
时可得:x1+x2=
=
,∴xG=
,代入y=-
×(x-2)=
G(
,
),直线OG的方程为:y=x,②
把②代入椭圆方程得:C(
),D(-
,-
),
三角形面积为:
×
|x1-x2|×h=
×|x1-x2|×h=
×h
h1=
,h2=
,
可知|S1-S2|=
×|
-
|=
×
=
当k=
时,同理得:|S1-S2|=
×|
-
|=
×
=
所以综上可得:|S1-S2|=
.
| x2 |
| 2 |
得到:(1+2k2)x2-8k2x+8k2-2=0①
又因为若点G的横坐标为
| 2 |
| 3 |
所以:x1+x2=
| 8k2 |
| 1+2k2 |
| 4 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
x1x2=
| 8k2-2 |
| 2k2+1 |
| 1+k2 |
所以l的方程:y=±
| 1 |
| 2 |
(2)把k2=
| 1 |
| 4 |
| 4 |
| 3 |
∵过点P(2,0)作直线l交椭圆
| x2 |
| 2 |
∴根据韦达定理,弦长公式;知x1x2=
| 8k2-2 |
| 2k2+1 |
| 1+k2 |
所以|AB|=×
| 1+k2 |
| ||
| 2 |
| 4 |
| 3 |
2
| ||
| 3 |
当k=-
| 1 |
| 2 |
| 8k2 |
| 1+2k2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
G(
| 2 |
| 3 |
| 2 |
| 3 |
把②代入椭圆方程得:C(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
三角形面积为:
| 1 |
| 2 |
| 1+k2 |
| ||
| 4 |
| ||
| 3 |
h1=
| ||
|
| ||
|
可知|S1-S2|=
| ||
| 3 |
| ||
|
| ||
|
| ||
| 3 |
| 4 | ||
|
| 4 |
| 3 |
当k=
| 1 |
| 2 |
| ||
| 3 |
| ||
|
| ||
|
| ||
| 3 |
| 4 | ||
|
| 4 |
| 3 |
所以综上可得:|S1-S2|=
| 4 |
| 3 |
点评:本题综合考查了运用方程解决直线和圆锥曲线的位置关系,及应用解决面积的问题,注意繁琐的运算.

练习册系列答案
相关题目
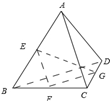 在空间四边形ABCD中,E、F、G分别在棱AB、BC、CD上,若AC∥面EFG,BD∥面EFG,
在空间四边形ABCD中,E、F、G分别在棱AB、BC、CD上,若AC∥面EFG,BD∥面EFG,