题目内容
已知二次函数f(x)=ax2+bx+c(a≠0),不等式f(x)<-2x的解集为{x|-3<x<-1}.若函数g(x)=f(x)+6a和x轴只有一个交点.
(1)求f(x)的解析式;
(2)当x∈[
,5]时,求函数y=f(x)的最小值.
(1)求f(x)的解析式;
(2)当x∈[
| 5 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用一元二次不等式与二次函数以及一元二次方程的关系得到系数的等式解之;
(2)由(1)可知二次函数的对称轴与区间的关系,然后求最小值.
(2)由(1)可知二次函数的对称轴与区间的关系,然后求最小值.
解答:
解:(1)∵不等式f(x)<-2x的解集为{x|-3<x<-1}.
∴ax2+(b+2)x+c=0的两个根是-3和-1,并且a>0,
∴9a-3(b+2)+c=0,①;a-(b+2)+c=0,②
又∵函数g(x)=f(x)+6a和x轴只有一个交点,
∴△=b2-4a(c+6a)=0③
由①②③解得a=
,b=-
,c=
,
∴f(x)=
x2-
x+
;
(2)由(1)得f(x)=
x2-
x+
=
(x-2)2-
;
∴当x∈[
,5]时,函数为增函数,∴函数y=f(x)的最小值为f(2)=-
.
∴ax2+(b+2)x+c=0的两个根是-3和-1,并且a>0,
∴9a-3(b+2)+c=0,①;a-(b+2)+c=0,②
又∵函数g(x)=f(x)+6a和x轴只有一个交点,
∴△=b2-4a(c+6a)=0③
由①②③解得a=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴f(x)=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
(2)由(1)得f(x)=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
∴当x∈[
| 5 |
| 2 |
| 1 |
| 5 |
点评:本题考查了“三个二次”之间的关系以及二次函数闭区间上的最值求法,注意明确对称轴与区间的位置关系,从而明确区间的单调性.

练习册系列答案
相关题目
设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,命题不正确的是( )
| A、当c⊥α时,若α∥β,则c⊥β |
| B、当b?α时,若α⊥β,则b⊥β |
| C、当b?α,a?α且c是a在α内的射影时,若a⊥b,则b⊥c |
| D、当b?α且c?α时,若b∥c,则c∥α |
y=|x2-2x-3|与y=k有4个不同的交点,则k的范围( )
| A、(-4,0) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
设数列{an}的前n项和为Sn,点(n,
)(n∈N*)均在函数y=
x+
的图象上,则a2014=( )
| Sn |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2014 | B、2013 |
| C、1012 | D、1011 |
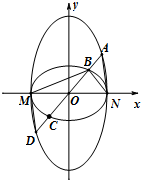 如图,曲线C1:
如图,曲线C1: