题目内容
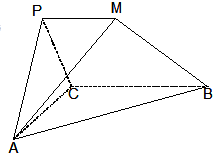在如图所示的多面体PMBCA中，平面PAC⊥平面ABC，△PAC是边长为2的正三角形，PM∥BC，且BC=2PM=4，AB=2| 5 |
（Ⅰ）求证：PA⊥BC；
（Ⅱ）求多面体PMBCA的体积．
考点：棱柱、棱锥、棱台的体积
专题：综合题,空间位置关系与距离
分析：（Ⅰ）先证明AC⊥BC，再利用平面PAC⊥平面ABC，证明BC⊥平面PAC，即可证明PA⊥BC；
（Ⅱ）作AD⊥PC于点D，证明AD⊥平面BCPM，求出四边形BCPM的面积，即可求多面体PMBCA的体积．
（Ⅱ）作AD⊥PC于点D，证明AD⊥平面BCPM，求出四边形BCPM的面积，即可求多面体PMBCA的体积．
解答：
（Ⅰ）证明：∵AC=2，BC=4，AB=2
，∴AC2+BC2=AB2，∴AC⊥BC
∵平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，
∴BC⊥平面PAC，
∵PA?平面PAC，∴BC⊥PA．…..（6分）
（Ⅱ）解：作AD⊥PC于点D．由（Ⅰ）知BC⊥平面PAC，∴BC⊥AD，BC⊥PC
又PM∥BC，且BC=2PM=4，∴四边形BCPM是上、下底分别为2、4，高为2的直角梯形，其面积为6．
又BC∩PC=C，∴AD⊥平面BCPM，AD=
．
故多面体PMBCA的体积为
×SBCPM×AD=
×6×
=2
．…..（13分）
| 5 |
∵平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，
∴BC⊥平面PAC，
∵PA?平面PAC，∴BC⊥PA．…..（6分）
（Ⅱ）解：作AD⊥PC于点D．由（Ⅰ）知BC⊥平面PAC，∴BC⊥AD，BC⊥PC
又PM∥BC，且BC=2PM=4，∴四边形BCPM是上、下底分别为2、4，高为2的直角梯形，其面积为6．
又BC∩PC=C，∴AD⊥平面BCPM，AD=
| 3 |
故多面体PMBCA的体积为
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
点评：本题考查面面垂直的性质，线面平行的判定，考查多面体PMBCA的体积，正确运用面面垂直的性质是关键．
练习册系列答案
阅读快车系列答案
相关题目
下列选项中，说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、命题“若am2＜bm2，则a＜b”的逆命题是真命题 |
| C、命题“?x∈R，x2-x+1≥0”的否定是：“?x0∈R，x02-x0+1≤0” |
| D、命题“若x=y，则cosx=cosy”的逆否命题为真命题 |
函数f（x）=
的导数是（ ）
| 1 |
| (3x-2)2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
如图所示，在正方体ABCD-A1B1C1D1中，E、F、G、H分别是BC、C1C、C1D1、A1A的中点．求证：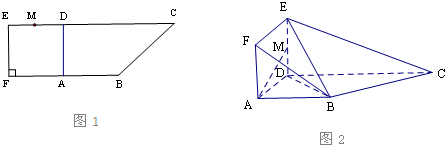
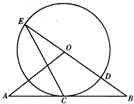如图，直线AB经过⊙O上一点C，且OA=OB，CA=CB，⊙O交直线OB于点E、D．
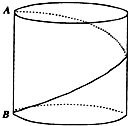如图，底面半径为1，高为2的圆柱，有A点有一只蚂蚁，现在这只蚂蚁要围绕圆柱由A点爬到B点，问蚂蚁爬行的最短距离是多少？
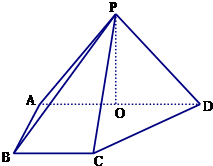如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=