题目内容
12．
一拱桥的形状为抛物线，该抛物线拱的高为h，宽为b，此抛物线拱的面积为S，若b=3h，则S等于（ ）| A． | h2 | B． | $\frac{3}{2}$h2 | C． | $\sqrt{3}$h2 | D． | 2h2 |
分析 建立平面直角坐标系，设抛物线方程，将点代入抛物线方程，即可求得抛物线方程，根据定积分的几何意义，即可求得S．
解答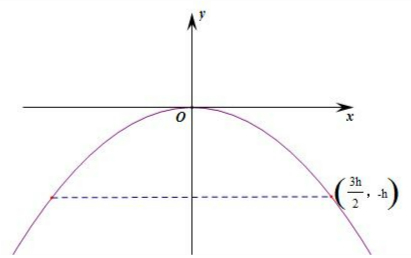 
解：以抛物线的最高点为坐标原点，以抛物线的拱的对称轴为y轴，建立平面直角坐标系，
设抛物线方程y=ax2，a＜0，
由抛物线经过点（$\frac{3h}{2}$，-h），代入抛物线方程：-h=a（$\frac{3h}{2}$）2，
解得：a=-$\frac{4}{9h}$，
S=h×3h-（-2${∫}_{0}^{\frac{3h}{2}}$ax2dx），=3h2-2×$\frac{4}{9h}$×$\frac{1}{3}$x3${丨}_{0}^{\frac{3h}{2}}$=2h2，
故选D．
点评 本题考查抛物线的方程，定积分的几何意义，利用定积分求曲边梯形的面积，考查数形结合思想，属于中档题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
2．已知文具盒中有5支铅笔，其中3支红色，2支黄色．现从这5只铅笔中任取2支，这两支铅笔颜色恰好不同的概率为（ ）
| A． | 0.4 | B． | 0.6 | C． | 0.8 | D． | 1 |
3．在长方体ABCD-A1B1C1D1的十二条棱中，与面对角线AC垂直且异面的棱的条数是（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
20．在△ABC中，a=$\sqrt{7}$，b=2，A=60°，则c=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
7．已知定义在R上的函数y=f（x）满足以下三个条件：
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称，则下列结论中正确的是（ ）
①对于任意的x∈R，都有f（x+4）=f（x）；
②对于任意的x1，x2∈R，且0≤x1＜x2≤2，都有f（x1）＜f（x2）；
③函数y=f（x+2）的图象关于y轴对称，则下列结论中正确的是（ ）
| A． | f（4.5）＜f（7）＜f（6.5） | B． | f（7）＜f（4.5）＜f（6.5） | C． | f（7）＜f（6.5）＜f（4.5） | D． | f（4.5）＜f（6.5）＜f（7） |
已知函数f（x）=sin（ωx+φ）（ω＞0）的图象如图所示，则f（4）=$\frac{\sqrt{2}}{2}$．