题目内容
已知箱子里装有4张大小、形状都相同的卡片,标号分别为1,2,3,4
(1)从箱子中任取两张卡片,求两张卡片的标号之和不小于4的概率;
(2)从箱子中任意取出一张卡片记下它的标号m,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号n,求使得幂函数f(x)=(m-n)x
的图象关于y轴对称的概率.
(1)从箱子中任取两张卡片,求两张卡片的标号之和不小于4的概率;
(2)从箱子中任意取出一张卡片记下它的标号m,然后再放回箱子中;第二次再从箱子中任取一张卡片,记下它的标号n,求使得幂函数f(x)=(m-n)x
| m |
| n |
考点:古典概型及其概率计算公式,幂函数的概念、解析式、定义域、值域,幂函数图象及其与指数的关系
专题:概率与统计
分析:(1)从箱子中任取两张卡片,共有
=6个事件(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).其中满足两张卡片的标号之和不小于4的有(1,3),(1,4),(2,3),(2,4),(3,4),共有5中情况.利用古典概型的概率计算公式即可得出.
(2)从箱子中有放回的取出两张卡片共有42=16种情况,其中使得幂函数f(x)=(m-n)x
的图象关于y轴对称的满足:m-n=1,m偶数,有以下两种情况:m=2,n=1;m=4,n=3.利用古典概型的概率计算公式即可得出.
| ∁ | 2 4 |
(2)从箱子中有放回的取出两张卡片共有42=16种情况,其中使得幂函数f(x)=(m-n)x
| m |
| n |
解答:
解:(1)从箱子中任取两张卡片,共有
=6个事件(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).其中满足两张卡片的标号之和不小于4的有(1,3),(1,4),(2,3),(2,4),(3,4),共有5中情况.因此其中满足两张卡片的标号之和不小于4的概率P=
.
(2)从箱子中有放回的取出两张卡片共有42=16种情况,其中使得幂函数f(x)=(m-n)x
的图象关于y轴对称的满足:m-n=1,m偶数,
有以下两种情况:m=2,n=1;m=4,n=3.
∴使得幂函数f(x)=(m-n)x
的图象关于y轴对称的概率P=
=
.
| ∁ | 2 4 |
| 5 |
| 6 |
(2)从箱子中有放回的取出两张卡片共有42=16种情况,其中使得幂函数f(x)=(m-n)x
| m |
| n |
有以下两种情况:m=2,n=1;m=4,n=3.
∴使得幂函数f(x)=(m-n)x
| m |
| n |
| 2 |
| 16 |
| 1 |
| 8 |
点评:本题考查了古典概型的概率计算公式、幂函数的性质,考查了推理能力,属于基础题.

练习册系列答案
相关题目
当曲线y=1-
与直线kx-y-3k+3=0有两个相异的交点时,实数k的取值范围是( )
| 4-x2 |
A、(0,
| ||
B、(
| ||
C、(0,
| ||
D、[2,
|
设α,β,γ是三个互不重合的平面,m,n是两条不重合的直线,则下列命题中正确的是( )
| A、若m∥α,n∥β,α⊥β,则m⊥n |
| B、若α∥β,m?β,m∥α,则m∥β |
| C、若α⊥β,m⊥α,则m∥β |
| D、若α⊥β,β⊥γ,则α⊥γ |
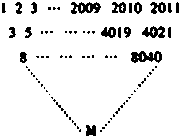 给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=
给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=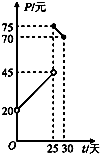 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表: