题目内容
20.平面直角坐标系中,已知O为坐标原点,点A、B的坐标分别为(1,1)、(-3,3).若动点P满足$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,其中λ、μ∈R,且λ+μ=1,则点P的轨迹方程为( )| A. | x-y=0 | B. | x+y=0 | C. | x+2y-3=0 | D. | (x+1)2+(y-2)2=5 |
分析 由已知向量等式可知P在AB所在的直线上,由直线方程的两点式得答案.
解答 解:由$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,且λ+μ=1,得$\overrightarrow{OP}=λ\overrightarrow{OA}+(1-λ)\overrightarrow{OB}$=$λ(\overrightarrow{OA}-\overrightarrow{OB})+\overrightarrow{OB}$,
∴$\overrightarrow{OP}-\overrightarrow{OB}=λ\overrightarrow{BA}$,即$\overrightarrow{BP}=λ\overrightarrow{BA}$,则P、A、B三点共线.
设P(x,y),则P在AB所在的直线上,
∵A(1,1)、B(-3,3),
∴AB所在直线方程为$\frac{y-1}{3-1}=\frac{x-1}{-3-1}$,整理得:x+2y-3=0.
故P的轨迹方程为:x+2y-3=0.
故选:C.
点评 本题考查共线向量基本定理的应用,考查轨迹方程的求法,考查数学转化思想方法,是中档题.

练习册系列答案
相关题目
8.已知函数f(x)是偶函数,f(x+1)是奇函数,且对任意的x1,x2∈[0,1],且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]<0,设a=f($\frac{82}{11}$),b=-f($\frac{50}{9}$),c=f($\frac{24}{7}$),则下列结论正确的是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>a>b |
5.函数f(x)=sin(ωx+φ)+$\sqrt{3}cos({ωx+φ})({ω>0})$的图象过(1,2),若f(x)相邻的零点为x1,x2且满足|x1-x2|=6,则f(x)的单调增区间为( )
| A. | [-2+12k,4+12k](k∈Z) | B. | [-5+12k,1+12k](k∈Z) | C. | [1+12k,7+12k](k∈Z) | D. | [-2+6k,1+6k](k∈Z) |
12.已知a≥0,函数f (x)=(x2-2ax)ex,若f (x)在[-1,1]上是单调减函数,则a的取值范围是( )
| A. | (0,$\frac{3}{4}$) | B. | ($\frac{1}{2}$,$\frac{3}{4}$) | C. | (0,$\frac{1}{2}$) | D. | [$\frac{3}{4}$,+∞) |
10.若O为坐标原点,已知实数x,y满足条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,在可行域内任取一点P(x,y),则|OP|的最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3}{2}$ |
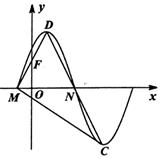 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.