题目内容
6.复数$\frac{5i}{{2+{i^9}}}$的共轭复数所对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数代数形式的乘除运算化简,再求其共轭复数,得到共轭复数的坐标得答案.
解答 解:∵$\frac{5i}{{2+{i^9}}}$=$\frac{5i}{2+i}=\frac{5i(2-i)}{(2+i)(2-i)}=1+2i$,
∴$\frac{5i}{{2+{i^9}}}$的共轭复数为1-2i,所对应的点的坐标为(1,-2),位于第四象限.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
16.若$\left\{\begin{array}{l}{sinθ<0}\\{tanθ>0}\end{array}\right.$ 则角θ所在的象限是( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
17.在复平面中,下列复数中所对应的点在第三象限的是( )
| A. | -1+2i | B. | -1-2i | C. | 3+2i | D. | 3-2i |
16.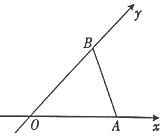 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
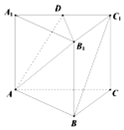 如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).
如图,在直三棱柱ABC-A1B1C1中,底面ABC为边长为2的正三角形,D是棱A1C1的中点,CC1=h(h>0).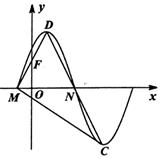 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.