题目内容
9.(1)计算:27${\;}^{\frac{2}{3}}$-$\sqrt{(3-π)^{2}}$+lg5+lg2;(2)化简:tan$\frac{5π}{4}$+sin($\frac{π}{2}$+α)-cos(-α)
分析 (1)由有理数指数幂的计算法则和对数的计算法则进行解答;
(2)根据诱导公式、特殊角的三角函数值进行解答.
解答 解:(1):27${\;}^{\frac{2}{3}}$-$\sqrt{(3-π)^{2}}$+lg5+lg2
=9-(π-3)+lg5×2
=9-π+3+1
=13-π;
(2)tan$\frac{5π}{4}$+sin($\frac{π}{2}$+α)-cos(-α)
=tan$\frac{π}{4}$+cosα-cosα
=1.
点评 本题主要考察了诱导公式的应用、有理数指数幂的化简求值,属于基本知识的考查.

练习册系列答案
相关题目
4.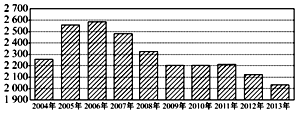 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )| A. | 逐年比较,2005年减少二氧化硫排放量的效果最显著 | |
| B. | 2008年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
1.已知集合A={1,3,$\sqrt{m}$},B={1,m},A∩B={1,m},则m=( )
| A. | 0或$\sqrt{3}$ | B. | 0或3 | C. | 1或3 | D. | 1或3或0 |
18.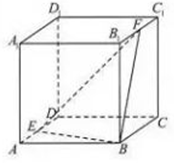 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )| A. | [0,1] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [1,2] | D. | [$\frac{3}{2}$,2] |