题目内容
14.设x,y∈[0,1],则满足y>$\sqrt{1-{x}^{2}}$的概率为( )| A. | 1-$\frac{π}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
分析 该题涉及两个变量,故是与面积有关的几何概型,分别表示出满足条件的面积和整个区域的面积,最后利用概率公式解之即可.
解答 解:由题意可得,x,y∈[0,1]的区域为边长为1的正方形,面积为1,
∵满足y>$\sqrt{1-{x}^{2}}$,x,y∈[0,1],其面积S=1-$\frac{π}{4}$,
∴x,y∈[0,1],则满足y>$\sqrt{1-{x}^{2}}$的概率为1-$\frac{π}{4}$,
故选A.
点评 本题主要考查了与面积有关的几何概率的求解,解题的关键是准确求出区域的面积,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
4.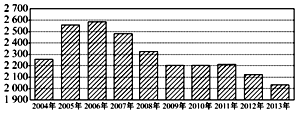 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
 我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )
我国一直为“低碳生活”努力,根据下面给出的2004年至2013年我国某有害物质排放量(单位:万吨)柱形图,以下结论正确的是( )| A. | 逐年比较,2005年减少二氧化硫排放量的效果最显著 | |
| B. | 2008年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
2.在等比数列{an}中,若a6=6,a9=9,则a3为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{16}{9}$ | D. | 4 |
6.下列四个命题中真命题为( )
| A. | lg(x2+1)≥0 | B. | 5≤2 | C. | 若x2=4,则x=2 | D. | 若x<2,则$\frac{1}{x}$>$\frac{1}{2}$ |
3.去A城市旅游有三条不同路线,甲、乙两位同学各自选择其中一条线路去A城市旅游,若每位同学选择每一条线路的可能性相同,则这两位同学选择同一条路线的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{9}$ |