题目内容
(1)若|cosθ|=-cosθ,且tanθ<0,试判断
的符号;
(2)若tan(cosθ)•tan(sinθ)>0,试求出θ所在象限,并用图形表示
的取值范围.
| sin(cosθ) |
| cos(sinθ) |
(2)若tan(cosθ)•tan(sinθ)>0,试求出θ所在象限,并用图形表示
| θ |
| 2 |
考点:三角函数值的符号
专题:三角函数的求值
分析:(1)由|cosθ|=-cosθ,且tanθ<0,可得θ在第二象限,即可判断出.
(2)由tan(cosθ)•tan(sinθ)>0,可得cosθ与sinθ同号,因此θ为第一象限或第三象限的角.则kπ<
<kπ+
或
+kπ<
<kπ+
(k∈Z).即可得出.
(2)由tan(cosθ)•tan(sinθ)>0,可得cosθ与sinθ同号,因此θ为第一象限或第三象限的角.则kπ<
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
| θ |
| 2 |
| 3π |
| 4 |
解答:
解:(1)∵|cosθ|=-cosθ,且tanθ<0,
∴θ在第二象限.
∴sin(cosθ)<0,cos(sinθ)>0,
∴
<0;
(2)∵tan(cosθ)•tan(sinθ)>0,
∴cosθ与sinθ同号,
∴θ为第一象限或第三象限的角.
则kπ<
<kπ+
或
+kπ<
<kπ+
(k∈Z).
用图形表示
的取值范围如图所示.

∴θ在第二象限.
∴sin(cosθ)<0,cos(sinθ)>0,
∴
| sin(cosθ) |
| cos(sinθ) |
(2)∵tan(cosθ)•tan(sinθ)>0,
∴cosθ与sinθ同号,
∴θ为第一象限或第三象限的角.
则kπ<
| θ |
| 2 |
| π |
| 4 |
| π |
| 2 |
| θ |
| 2 |
| 3π |
| 4 |
用图形表示
| θ |
| 2 |
点评:本题考查了三角函数值与所在象限的符号问题、三角函数的单调性,考查了推理能力,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m,n]上的最大值为2,则m+n=( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
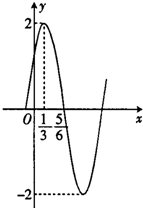 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<