题目内容
函数y=
ln(4-x2)的单调增区间是 ．
| 1 |
| 2 |
考点：对数函数的单调区间
专题：计算题,函数的性质及应用
分析：令f（x）=4-x2（-2≤x≤2），则f（x）在区间（-2，0]上单调递增，利用复合函数的性质即可求得答案．
解答：
解：∵4-x2＞0，
∴-2≤x≤2，
令f（x）=4-x2（-2≤x≤2），
则f（x）为开口向下的抛物线（一部分），其对称轴为x=0，
∴f（x）在区间（-2，0]上单调递增，又y=lnx为定义域上的增函数，
∵复合函数y=
ln（4-x2）在区间（-2，0]上单调递增，
故答案为：（-2，0]．
∴-2≤x≤2，
令f（x）=4-x2（-2≤x≤2），
则f（x）为开口向下的抛物线（一部分），其对称轴为x=0，
∴f（x）在区间（-2，0]上单调递增，又y=lnx为定义域上的增函数，
∵复合函数y=
| 1 |
| 2 |
故答案为：（-2，0]．
点评：本题考查复合函数的单调区间，求得f（x）=4-x2（-2≤x≤2）的单调递增区间是关键，考查分析与运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
函数g（x）=lnx-
的零点所在区间是（ ）
| 1 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
若集合A={x∈R|y=lg（2-x）}，B={y∈R|y=2x-1，x∈A}，则∁R（A∩B）=（ ）
| A、R |
| B、（-∞，0]∪[2，+∞） |
| C、[2，+∞） |
| D、（-∞，0] |
如图，已知椭圆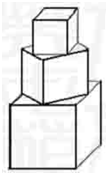
有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边中点，已知最底层正方体的棱长为2，且该塔形的表面积（含C最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是已知三角形ABC中，
•
＜0，则三角形ABC的形状为（ ）
| BA |
| BC |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰直角三角形 |