题目内容
如果f(n)=1+
+
+…+
+
…+
(n∈N*),那么f(k+1)-f(k)共有 项.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
考点:归纳推理
专题:点列、递归数列与数学归纳法
分析:根据f(n)的表达式,分别求出f(k+1),f(k)的表达式,即可求出结论.
解答:
解:∵f(n)=1+
+
+…+
+
…+
(n∈N*),
∴f(k)=1+
+
+???+
,
f(k+1)=1+
+
+???+
+
+???+
,
∴f(k+1)-f(k)=
+???+
=
+???+
,
∴共有2k项.
故答案为:2k.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
∴f(k)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k |
f(k+1)=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
∴f(k+1)-f(k)=
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2k+2k |
∴共有2k项.
故答案为:2k.
点评:本题主要考查数列的项的计算,根据归纳推理的应用,求出f(k+1),f(k)的表达式是解决本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
直线
x+y-2=0与圆x2+y2=4相交所得的弦的长为( )
| 3 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
已知a>0,x,y满足约束条件
,若z=2x+y的最小值为
,则a=( )
|
| 3 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
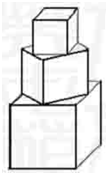 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是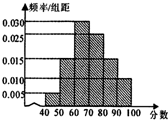 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为