题目内容
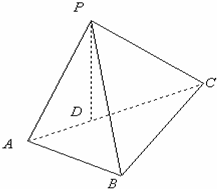 如图,三棱锥P-ABC,D为AC的中点,PA=PB=PC=
如图,三棱锥P-ABC,D为AC的中点,PA=PB=PC=| 5 |
| 2 |
| 2 |
| 6 |
(1)求证:PD⊥底面ABC;
(2)求二面角P-AB-C的正切值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件条件出PD⊥AC,PD⊥BD,由此能证明PD⊥底面ABC.
(2)过点D作DE⊥AB,连结PE,由三垂线定理知∠PED是二面角P-AB-C的平面角,由此能求出二面角P-AB-C的正切值.
(2)过点D作DE⊥AB,连结PE,由三垂线定理知∠PED是二面角P-AB-C的平面角,由此能求出二面角P-AB-C的正切值.
解答:
(1)证明:连结BD,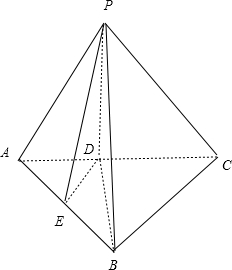
∵三棱锥P-ABC,D为AC的中点,PA=PB=PC=
,
AC=2
,AB=
,BC=
,
∴PD⊥AC,AB⊥BC,
∴BD=
AC=
,PD=
=
,
∴BD2+PD2=PB2,∴PD⊥BD,
∵AC∩BD=D,
∴PD⊥底面ABC.
(2)解:由(1)知PD⊥底面ABC,
过点D作DE⊥AB,连结PE,
由三垂线定理知∠PED是二面角P-AB-C的平面角,
∵D是AC的中点,∴DE是△ABC的中位线,
∴DE=
BC=
,
∴tan∠PED=
=
=
.
∴二面角P-AB-C的正切值为
.
故答案为:
.

∵三棱锥P-ABC,D为AC的中点,PA=PB=PC=
| 5 |
AC=2
| 2 |
| 2 |
| 6 |
∴PD⊥AC,AB⊥BC,
∴BD=
| 1 |
| 2 |
| 2 |
| 5-2 |
| 3 |
∴BD2+PD2=PB2,∴PD⊥BD,
∵AC∩BD=D,
∴PD⊥底面ABC.
(2)解:由(1)知PD⊥底面ABC,
过点D作DE⊥AB,连结PE,
由三垂线定理知∠PED是二面角P-AB-C的平面角,
∵D是AC的中点,∴DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠PED=
| PD |
| DE |
| ||||
|
| 2 |
∴二面角P-AB-C的正切值为
| 2 |
故答案为:
| 2 |
点评:本题考查直线与底面垂直的证明,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
在△ABC中,若sin2C=sin2A+sin2B则△ABC的形状一定是( )
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |

 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点F在PA上,且AF=2FP.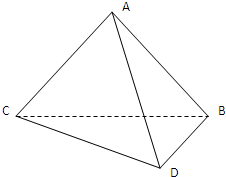 如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°
如图,平面ABC⊥平面DBC,已知AB=AC,BC=6,∠BAC=∠DBC=90°,∠BDC=60°