题目内容
求使
有意义的x的取值范围．
| 3+2x+x2 |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求出函数的定义域．
解答：
解：要使函数有意义，则3+2x+x2≥0，
∵x2+2x+3=（x+1）2+2≥2，
∴3+2x+x2≥0恒成立，
即x的取值范围是R．
∵x2+2x+3=（x+1）2+2≥2，
∴3+2x+x2≥0恒成立，
即x的取值范围是R．
点评：本题主要考查函数定义域的求法，根据函数成立的条件是解决本题的关键．
练习册系列答案
相关题目
函数y=2sin（x+φ）的图象为C，则以下判断中，正确的是（ ）
A、过点（
| ||
B、过点（-
| ||
| C、在长度为2π的闭区间上恰有一个最高点和一个最低点 | ||
| D、图象C关于原点对称 |
将曲线的极坐标方程ρsinθ=4化为直角坐标方程为（ ）
| A、x-4=0 |
| B、y-4=0 |
| C、x+4=0 |
| D、y+4=0 |
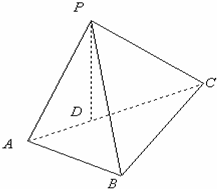如图，三棱锥P-ABC，D为AC的中点，