题目内容
设命题p：函数f（x）=lg（ax2-x+
a）的定义域为R，命题q：不等式
＜1+ax对一切正实数x均成立，如果命题p∨q为真，p∧q为假，求实数a的取值范围．
| 1 |
| 16 |
| 3x+1 |
考点：复合命题的真假
专题：简易逻辑
分析：由二次函数和不等式的性质分别可得p真和q真时的a的取值范围，再由建议逻辑可得得
，或
，由集合的运算可得．
|
|
解答：
解：p为真等价于ax2-x+
a＞0恒成立，
当a=0时不合题意，∴
，解得a＞2；
q为真等价于a＞
=
=
对一切x＞0恒成立，
又
+1＞2，∴
＜
，∴a≥
，
又命题p∨q为真，p∧q为假可得
，或
，
∴
，或
，综合可得
≤a≤2
| 1 |
| 16 |
当a=0时不合题意，∴
|
q为真等价于a＞
| ||
| x |
| 3x | ||
x(
|
| 3 | ||
|
又
| 3x+1 |
| 3 | ||
1+
|
| 3 |
| 2 |
| 3 |
| 2 |
又命题p∨q为真，p∧q为假可得
|
|
∴
|
|
| 3 |
| 2 |
点评：本题考查复合命题的真假，涉及恒成立问题，属基础题．
练习册系列答案
相关题目
若不等式5x2-bx+c＜0 的解集为{x|-1＜x＜3}，则b+c的值为（ ）
| A、5 | B、-5 | C、-25 | D、10 |
函数y=2x3-12x在区间[-1，3]上的最大值和最小值分别为（ ）
A、18，-8
| ||||
| B、54，-12 | ||||
C、8
| ||||
D、10，-8
|
将曲线的极坐标方程ρsinθ=4化为直角坐标方程为（ ）
| A、x-4=0 |
| B、y-4=0 |
| C、x+4=0 |
| D、y+4=0 |
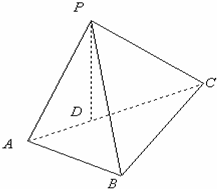如图，三棱锥P-ABC，D为AC的中点，