题目内容
在△ABC中，若sin2C=sin2A+sin2B则△ABC的形状一定是（ ）
| A、等腰直角三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等边三角形 |
考点：正弦定理
专题：解三角形
分析：由条件利用正弦定理可得 c2=a2+b2，可得△ABC的形状一定是直角三角形．
解答：
解：△ABC中，∵sin2C=sin2A+sin2B，∴由正弦定理可得 c2=a2+b2，
故△ABC的形状一定是直角三角形，
故选：C．
故△ABC的形状一定是直角三角形，
故选：C．
点评：本题主要考查正弦定理的应用，属于基础题．
练习册系列答案
口算能手系列答案
相关题目
若-16，a，b，c，-1成等比数列，那么（ ）
| A、b=4，ac=16 |
| B、b=-4，ac=16 |
| C、b=4，ac=-16 |
| D、b=-4，ac=-16 |
若不等式5x2-bx+c＜0 的解集为{x|-1＜x＜3}，则b+c的值为（ ）
| A、5 | B、-5 | C、-25 | D、10 |
函数y=2sin（x+φ）的图象为C，则以下判断中，正确的是（ ）
A、过点（
| ||
B、过点（-
| ||
| C、在长度为2π的闭区间上恰有一个最高点和一个最低点 | ||
| D、图象C关于原点对称 |
下列说法错误的是（ ）
| A、如果命题“?p”与命题“p或q”都是真命题，那么命题q一定是真命题． |
| B、命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0” |
| C、命题p：?x0∈R，x02-2x0+4＜0，则?p：?x∈R，x2-2x+4≥0 |
| D、特称命题“?x∈R，使-2x2+x-4=0”是真命题． |
在等差数列{an}中，前15项的和S15=90，则a8为（ ）
| A、6 | B、3 | C、12 | D、4 |
函数y=2x3-12x在区间[-1，3]上的最大值和最小值分别为（ ）
A、18，-8
| ||||
| B、54，-12 | ||||
C、8
| ||||
D、10，-8
|
将曲线的极坐标方程ρsinθ=4化为直角坐标方程为（ ）
| A、x-4=0 |
| B、y-4=0 |
| C、x+4=0 |
| D、y+4=0 |
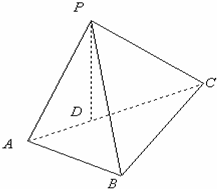如图，三棱锥P-ABC，D为AC的中点，