题目内容
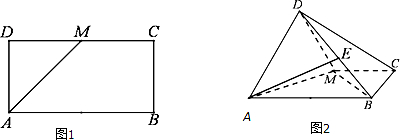
如图1,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM,如图2所示.

(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,三棱锥M-ADE的体积为
.

(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,三棱锥M-ADE的体积为
| ||
| 12 |
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)AD⊥BM?BD⊥面ADM?
?在矩形ABCD中,AB=2且AD=1;
(2)三棱锥M-ADE的体积就是三棱锥E-ADM的体积,而三角形ADM面积已知,则可以算出三棱锥E-ADM的高h,又由(1)可知,BM⊥面ADM,通过h与BM的比值可确定E点在BD上的位置.
|
(2)三棱锥M-ADE的体积就是三棱锥E-ADM的体积,而三角形ADM面积已知,则可以算出三棱锥E-ADM的高h,又由(1)可知,BM⊥面ADM,通过h与BM的比值可确定E点在BD上的位置.
解答:
 (本小题满分12分)
(本小题满分12分)
(1)连接BM,矩形ABCD中,AB=2,AD=1,M为CD中点,AM=BM=
,
由勾股定理得BM⊥AM;
折起后,平面ADM⊥平面ABCM,且平面ADM∩平面ABCM=AM,BM?平面ABCM;
得BM⊥平面ADM,
又AD?平面ADM,所以AD⊥BM;
(2)在△BDM中,作EF∥BM交DM于F.
(1)中已证明BM⊥平面ADM,∴EF⊥平面ADM,EF是三棱锥E-MAD的高,
VM-ADE=VE-MAD=
(
AD•DM)•EF=
,∴EF=
,
∴△DMB中,BM=
,且EF∥BM,
∴EF为中位线,E为BD的中点.
 (本小题满分12分)
(本小题满分12分)(1)连接BM,矩形ABCD中,AB=2,AD=1,M为CD中点,AM=BM=
| 2 |
由勾股定理得BM⊥AM;
折起后,平面ADM⊥平面ABCM,且平面ADM∩平面ABCM=AM,BM?平面ABCM;
得BM⊥平面ADM,
又AD?平面ADM,所以AD⊥BM;
(2)在△BDM中,作EF∥BM交DM于F.
(1)中已证明BM⊥平面ADM,∴EF⊥平面ADM,EF是三棱锥E-MAD的高,
VM-ADE=VE-MAD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 12 |
| ||
| 2 |
∴△DMB中,BM=
| 2 |
∴EF为中位线,E为BD的中点.
点评:折叠问题一般是重点分析折叠后未变的平行与垂直关系,线段的长,角度的不变的量;作为探究性问题,先把结论当成已知,然后结合已知条件列出方程求解,若有符合题意的解,则结论成立,否则不成立.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
下列说法错误的是( )
| A、如果命题“?p”与命题“p或q”都是真命题,那么命题q一定是真命题. |
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” |
| C、命题p:?x0∈R,x02-2x0+4<0,则?p:?x∈R,x2-2x+4≥0 |
| D、特称命题“?x∈R,使-2x2+x-4=0”是真命题. |
 如图,三棱锥P-ABC,D为AC的中点,
如图,三棱锥P-ABC,D为AC的中点, 如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.