题目内容
设f(n)是定义在N*上的增函数,f(4)=5,且满足:①任意n∈N*,f(n)∈Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
(1)求f(1),f(2),f(3)的值;
(2)求f(n)的表达式.
考点:抽象函数及其应用
专题:综合题,函数的性质及应用
分析:(1)利用已知的表达式,通过m=1,n=4,直接求f(1),利用函数的单调性以及f(n)∈Z,即可求出f(2),f(3)的值;
(2)利用函数的关系式,推出f(n+1)≤n+2,又f(n+1)≥n+2,然后求出f(n)的表达式.
(2)利用函数的关系式,推出f(n+1)≤n+2,又f(n+1)≥n+2,然后求出f(n)的表达式.
解答:
解:(1)∵f(m)f(n)=f(mn)+f(m+n-1),f(4)=5,
∴f(1)f(4)=f(4)+f(4).
∴5f(1)=10,∴f(1)=2;
∵f(n)是定义在N*上的增函数,
∴2=f(1)<f(2)<f(3)<f(4)
∵f(n)∈Z,
∴f(2)=3,f(3)=4.
(2)∵f(n)是定义在N*上的增函数,
∴f(n+1)>f(n),又f(n)∈Z,
∴f(n+1)≥f(n)+1,又f(1)=2.∴f(n)≥n+1,
由已知可得:f(2)f(n)=f(2n)+f(n+1),
而f(2)=3,f(2n)≥2n+1,
∴3f(n)≥f(n+1)+2n+1,
即f(n+1)≤3f(n)-2n-1或者f(n+1)-n-2≤3(f(n)-n-1)
∴有f(n+1)-n-2≤3(f(n)-n-1)≤32(f(n-1)-n)≤33(f(n-2)-n+1)≤…≤3n(f(1)-2)=0
于是,f(n+1)≤n+2,又f(n+1)≥n+2,
∴f(n+1)=n+2.
又f(1)=2,
∴f(n)=n+1.
∴f(1)f(4)=f(4)+f(4).
∴5f(1)=10,∴f(1)=2;
∵f(n)是定义在N*上的增函数,
∴2=f(1)<f(2)<f(3)<f(4)
∵f(n)∈Z,
∴f(2)=3,f(3)=4.
(2)∵f(n)是定义在N*上的增函数,
∴f(n+1)>f(n),又f(n)∈Z,
∴f(n+1)≥f(n)+1,又f(1)=2.∴f(n)≥n+1,
由已知可得:f(2)f(n)=f(2n)+f(n+1),
而f(2)=3,f(2n)≥2n+1,
∴3f(n)≥f(n+1)+2n+1,
即f(n+1)≤3f(n)-2n-1或者f(n+1)-n-2≤3(f(n)-n-1)
∴有f(n+1)-n-2≤3(f(n)-n-1)≤32(f(n-1)-n)≤33(f(n-2)-n+1)≤…≤3n(f(1)-2)=0
于是,f(n+1)≤n+2,又f(n+1)≥n+2,
∴f(n+1)=n+2.
又f(1)=2,
∴f(n)=n+1.
点评:本题考查抽象函数的解析式的应用,函数值的求法,放缩法的应用,考查逻辑推理能力以及计算能力.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
设
,
是非零向量,则“
-
=
”是“
∥
”的( )
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
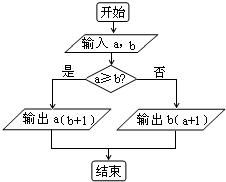
对于实数a和b,定义运算a*b,运算原理如图所示,则式子(
)-2*lne2的值为( )
| 1 |
| 2 |

| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,D、E、F分别是PC、AC、BC的中点.