题目内容
已知P={x||1-
|≤2},Q={x|x2-2x+(1-m2)≤0},其中m>0,全集U=R.若“x∈∁UP”是“x∈∁UQ”的必要不充分条件,求实数m的取值范围.
| x-1 |
| 3 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义和关系,结合不等式的关系,即可得到结论.
解答:
解:由“x∈∁UP”是“x∈∁UQ”的必要不充分条件,
可得∁UP?∁UQ,即P?Q,
P={x||1-
|≤2}={x|-2≤x≤10},Q={x|x2-2x+(1-m2)≤0}={x|1-m≤x≤1+m},
则
,
即
,解得m≥9,
故实数m的取值范围[9,+∞).
可得∁UP?∁UQ,即P?Q,
P={x||1-
| x-1 |
| 3 |
则
|
即
|
故实数m的取值范围[9,+∞).
点评:本题主要考查充分条件和必要条件的应用,根据不等式的解法求出集合是解决本题的关键.

练习册系列答案
相关题目
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(-1)=( )
| A、3 | B、1 | C、-1 | D、-3 |
设全集U={1,2,3,4,5,6,7,8},集合S={1,3,5},T={3,6},则∁U(S∪T)等于( )
| A、{2,4,7,8} |
| B、∅ |
| C、{1,3,5,6} |
| D、{2,4,6,8} |
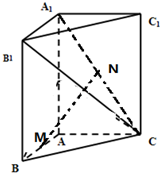 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.